データ収集の際に欠損のないように努力することが重要であることは言うまでもありませんが、どうしてもデータの欠損は出てしまうことが多いです。
データの欠損がある場合、真の結果をゆがめてしまう可能性があります。
ここでは欠損の種類と対処方法について述べていきます。
どういう場合に欠損が起こるか?
まずはデータの欠損が起こる具体的な状況を考えてみましょう。
・患者に配布した自記式質問票が無回答だった。
・検査を行っておらず、検査値が得られなかった。
・医師がカルテ記載をしておらず、身体所見に関するデータが得られなかった。
・医療機関への受診が途絶えてしまったため研究から脱落し、アウトカムに関する情報が得られなかった。
欠損の種類
欠損の種類は上記の3種類に分類されます。
| 欠損の種類 | 特徴 |
| missing completely at random (MCAR) | 完全にランダムな欠損。 例)特に理由もなく、たまたま年収の項目の回答が漏れてしまった。 Complete case analysis(完全ケース分析)でもバイアスを生じない。 |
| missing at random(MAR) | 欠損値が他の変数に依存する。 例)高齢であると、年収の項目に回答しない。 観察されている値は欠損値を予測するのに使うことができる。MCARよりも現実的。 |
| not missing at random (NMAR) | 欠損値がその変数自体に依存する。 例)年収が低いと、年収の項目に回答しない。 統計的な手法で対処するのは困難。 |
MCARであればバイアスを生じず無害な欠損と言えますが、実際のデータでそのような欠損が起きることは稀で何らかの規則性を持った欠損となってしまうことが多いです。
解析する際にはMARを仮定して行うことが多いです。(NMARは制御できないので)
欠損がある場合の解析方法
解析方法は大きく分けて、以下の3通りです。
| 解析方法 | 特徴 |
| 完全ケース分析 | 欠損がある対象者を除いて解析する。多変量解析ではモデルに入れたすべての変数がそろっている人のみ、対象に含まれる。 解析ソフトでは、通常、完全ケース分析が自動で実行される。 サンプルサイズが減少し、検出力が低下してしまう。 MCARでなければバイアスを生じてしまう可能性があり、バイアスの方向性も予測不能。 |
| 単一代入法 | 欠損に単一の値(回帰モデルから算出した予測値、平均値、ランダムな値など)を代入し、解析を行う。 MARの欠損による偏りを是正するが、甘い推定(差を人工的に大きくしてしまう可能性がある推定)となってしまう。 |
| 多重代入法 | MAR(もしくはCMAR)を仮定し、観測データを条件として欠損データの事後予測分布を構築して、そこから独立かつ無作為な 抽出を実行する(M個の代入済データセットができる)。M個のシミュレーションデータを分析し、結果を統合する。 保守的な推定(差を人工的に大きくしすぎない控えめな推定)となる。 |
多重代入法が最も適切な方法と言えます。
多重代入法のイメージは下図の通りです。
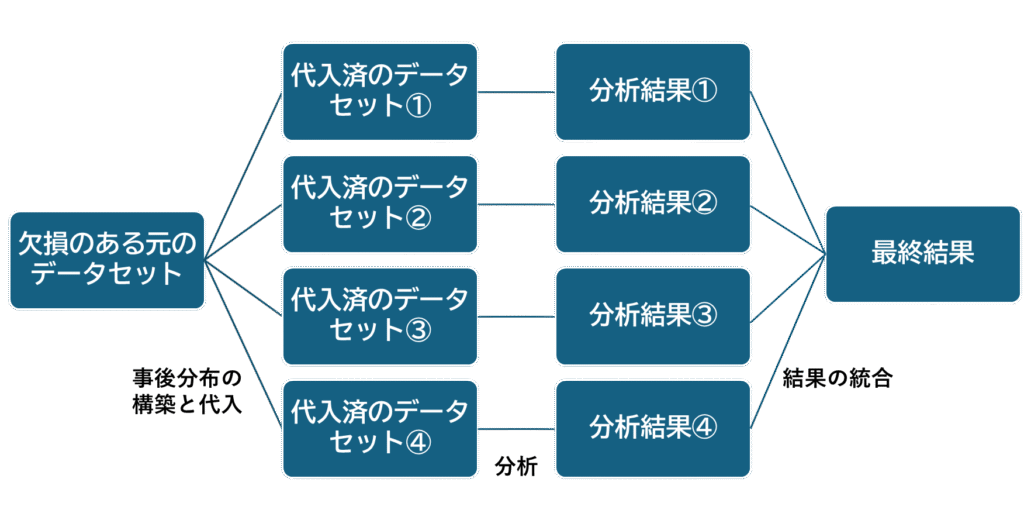
多重代入法はいつ使う?
上述のようにMCARな欠損は稀であるため、欠損がある場合、基本的にはMARを仮定して、多重代入法を行うのがよいとされています。でも解析が複雑になるし、面倒ですよね。
ただ、欠損率がどれくらいの場合に使うとよいか(完全ケース分析ではだめか)記載されているものはなかなか見当たりません。欠損のシミュレーションでは、データの20~25%を欠損させて用いているものが多く、20%を超える場合には多重代入法を用いて分析を行うのがよいと思われます。
それ以下であっても使うに越したことはないと思います。


コメント