EZRで単変量解析①－t検定とMann-Whitney検定

従属変数が2値数、独立変数が連続変数の場合はt検定、Mann-Whitney検定を行っていきます。独立変数が正規分布に準ずる場合はt検定、正規分布を想定できない場合はMann-Whitney検定を用います。検定の選択についてはこちら>>検定方法　いつ何を使う？

t検定

t検定は2群の平均に差があるかをみるために使います。
この例では年齢（Age）の平均値を再入院（ad2）の有無で比較します。
統計解析➡連続変数の解析➡2群間の平均値の比較（t検定）

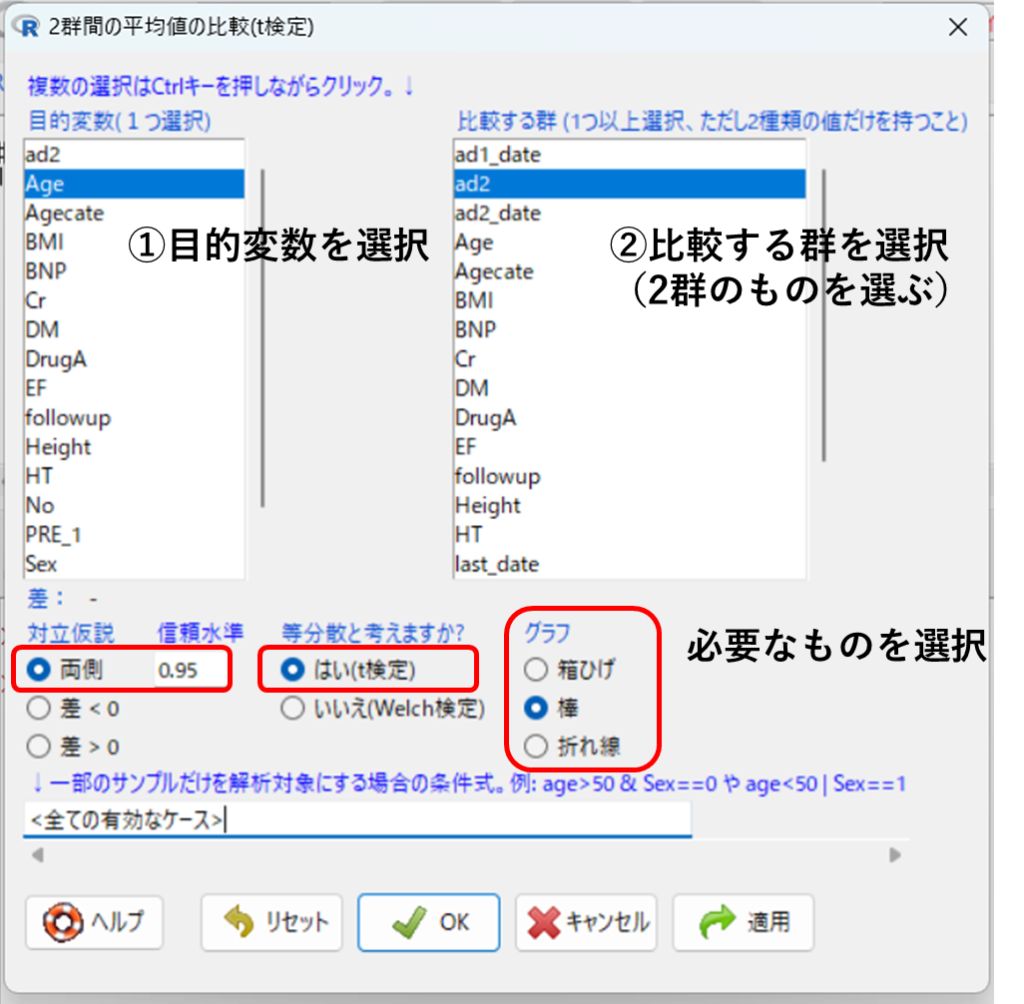
目的変数でAgeを選択し、比較する群でad2を選択します。比較する群は2値数である必要があります。
対立仮説では基本的には「両側」、有意水準「0.95」を選択し、等分散と考えますか？では「はい（t検定）」を選択します。グラフは必要なものを選択し、[OK]をクリックすると図2のように出力されます。

再入院あり群（ad2=1）、再入院なし群（ad2=0）で年齢の平均値と標準偏差が算出されます。統計学的な有意差はないことがわかります。

正規分布が仮定できない場合はノンパラメトリック検定であるMann-Whitney検定を行います。
この例ではCr値を再入院（ad2）の有無で比較します。
統計解析➡ノンパラメトリック検定➡2群間の比較（Mann-Whitney検定）

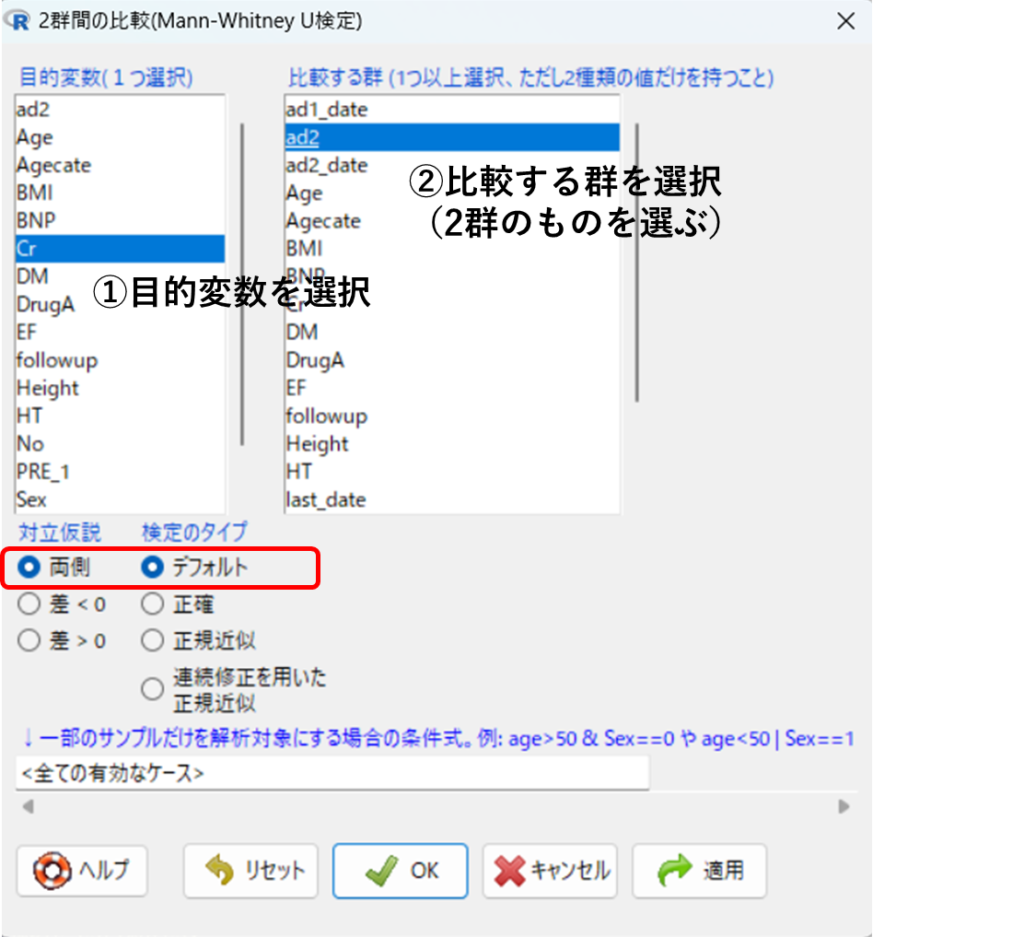
目的変数でCrを選択し、比較する群でad2を選択します。比較する群は2値数である必要があります。
対立仮説では基本的には「両側」、検定のタイプは「デフォルト」を選択します。[OK]をクリックすると図4のように出力されます。

再入院あり群（ad2=1）、再入院なし群（ad2=0）でCrの中央値と25パーセンタイル、75パーセンタイルが算出されます。統計学的な有意差はないことがわかります。

記述統計のときと同様、正規分布する場合は平均値±標準偏差、しない場合は中央値（25パーセンタイルー75パーセンタイル）で報告します。