3群間で検定を行う場合、2群間の検定を3回行うことには問題があり、t検定やMann-Whitney検定を用いることはできません。
今回は繰り返し検定の問題点と3群間の比較(分散分析)の考え方を勉強していきます。
SPSSで実際に検定する場合はこちら>>SPSSで3群間の比較 one way ANOVA & Kruskal-Wallis
繰り返し検定の問題点
A、B、Cの3群で連続変数の比較を行うこととします。これにはA vs B, B vs C, C vs Aの組み合わせがあります。この3つの組み合わせでt検定(有意水準5%)を繰り返すとします。
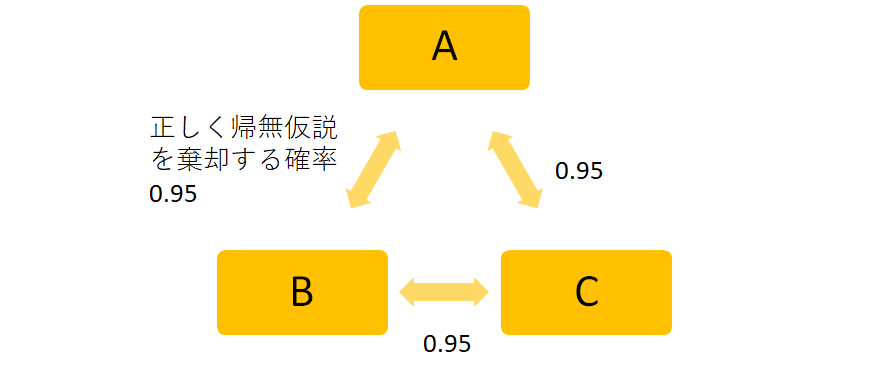
それぞれの組み合わせに対して正しく帰無仮説を棄却できるの確率は0.95です。そのため、3回とも正しく帰無仮説を棄却するためには
0.95×0.95×0.95=0.8573…
1-0.857…=0.1426…
つまり、有意水準5%で3回検定を行うと、有意水準は約14%まで下がってしまいます。それが繰り返し検定を行うことの問題点です。
分散分析(ANOVA) 一元配置分散分析の考え方
そこで用いるのが分散分析(Analysis of variance:ANOVA)です。ここでは一つの因子での比較を行う一元配置分散分析の考え方をみていきます。
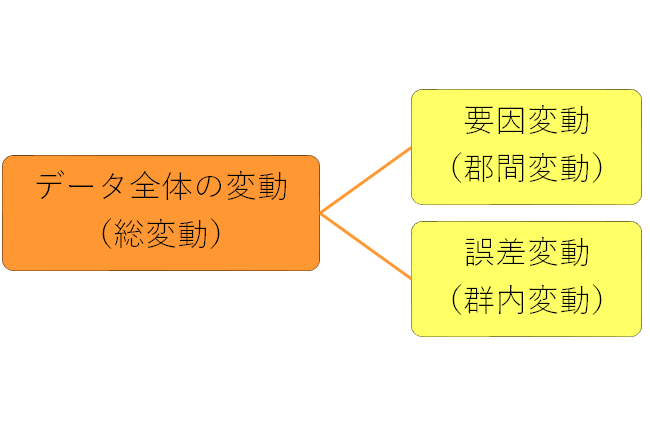
例として生後0日のネズミに3種類(A、B、C)の異なるエサを与え、生後30日時点での体重に違いがあるかという研究をするとします。 分散分析の基本的な考え方は、「データの変動(総変動)は要因変動(群間変動)と誤差変動(郡内変動)に分けられる」ということです。
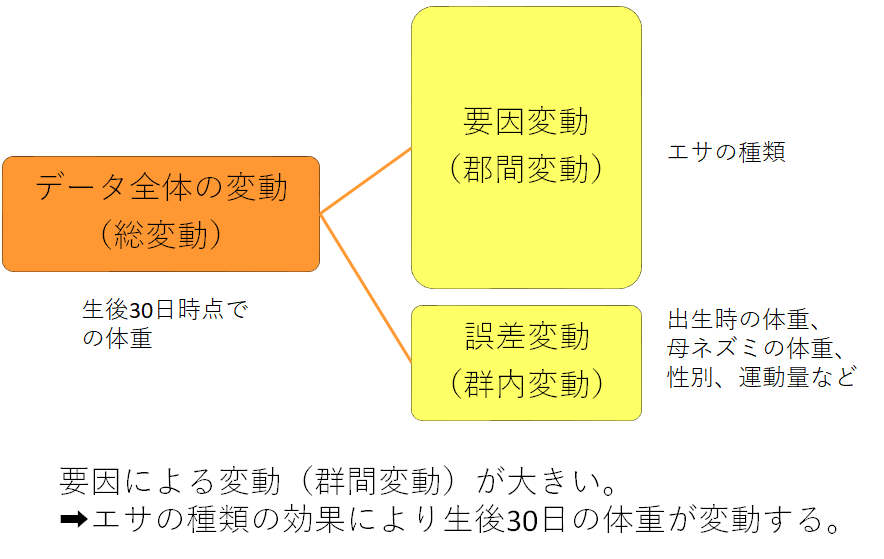
この例では要因変動はエサの種類、誤差変動は出生時の体重、母ネズミの体重、性別、運動量など生後30日時点での体重に影響するさまざまな因子が考えられます。
誤差変動に対して要因変動が大きければ、要因によってデータが変化するということが言えます。エサ以外の他の要因による体重の変動に対して、エサという要因による体重の変動が大きければ、「エサの効果で体重が変動する」ということが言えます。
群間変動の分散を群内変動の分散で割った統計量をF値と言います。
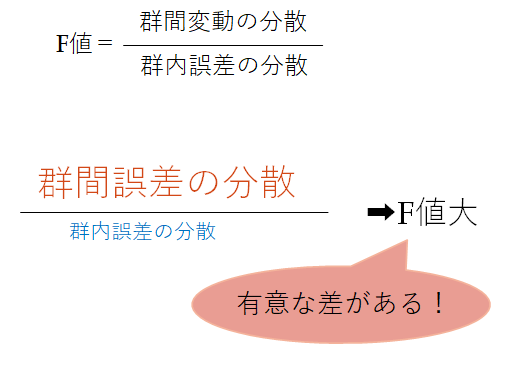
つまり、群間変動が大きい場合にF>1、群間変動が小さく、他の誤差変動に埋もれてしまう場合はF<1となります。
このF分布を用いて検定したものが一元配置分散分析となります。帰無仮説は「要因効果と誤差効果に差がない。」です。3群のどこにも差がない場合、帰無仮説は棄却され、3群のどこか(A vs B, B vs C, C vs A)に差がある場合には帰無仮説は棄却されません。
多重比較法(post hoc test)
一元配置分散分析では群のどこに差があるかはこの検定ではわかりません。多重比較法 (post hoc test)を用いる必要があります。
多重比較法にはさまざまな方法があり、分布調整型(検定につかう分布を厳しく調整する)、統計量調整型(統計量自体を調整する)、有意水準調整型(有意水準を厳しく調整する)に分けられます。
有名なBonferroniは統計全体の有意水準を、比較する組み合わせの数で割ります。例えば3群の検定であれば、組み合わせは3つなので0.05/3=0.0167となり、有意水準1.7%とします。比較する群が増えれば増えるほど有意水準が厳しくなって有意差が出にくくなるという欠点があります。 Turkeyの方法は分布調整型に分類され、不偏誤差分散を用いて調整します。こちらは汎用性が高く、使いやすいと思います。


コメント