論文ではオッズ比が多用されており、アウトカムが2値数のときにロジスティック回帰分析を使用してオッズ比を算出している方も多いのではないでしょうか?オッズ比はとても使いやすい一方、間違った解釈がなされていることがあります。ここではオッズ比とは何か、オッズ比を解釈する際の注意点を確認しましょう。
オッズ比とは?リスク比との違い
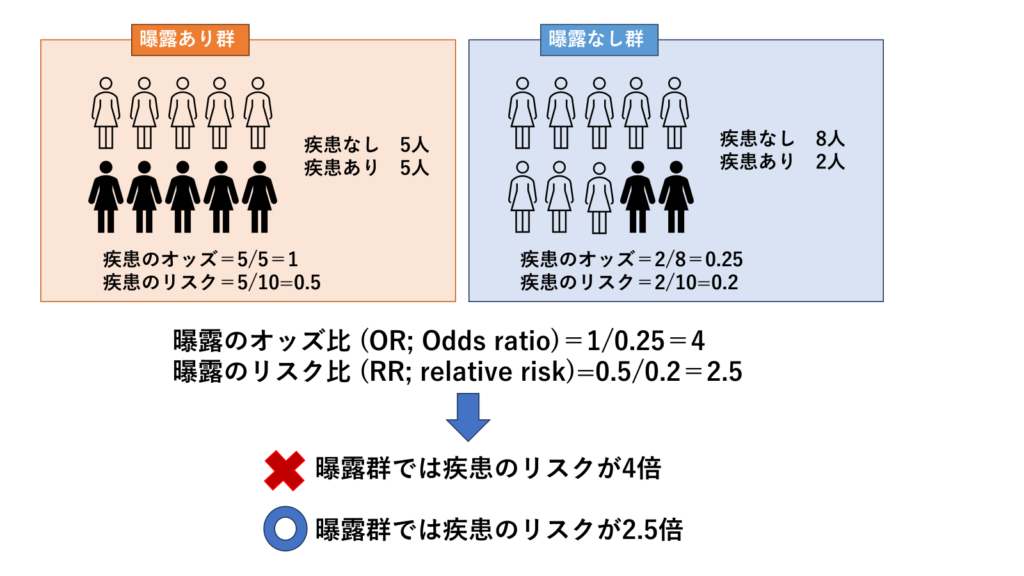
オッズ比は「比(Ratio)」、リスク比は「Proportion」であり、見ているものが異なります。
リスク比はそのまま「リスクが2.5倍」と解釈できますが、オッズ比では単純に「リスクは○倍」と解釈することは困難です。
オッズ比のメリット
解釈が難しいにも関わらず、オッズ比が多用される理由として下記のようなメリットがあるためです。

②のように、アウトカムの発症率が10%未満の比較的まれな疾患の場合は、オッズ比はリスク比と近似することができます。それ以上になると、オッズ比が跳ね上がってしまい、リスク比よりも高く算出される傾向にあるので注意が必要です。上の例でも全体の疾患発症率は7/20=0.35(35%)であり、10%を上回っています。オッズ比>リスク比となっていますよね。
③「〇倍」と具体的な数で比較することはできませんが、複数の曝露に対して大小の比較は可能です。
④ロジスティック回帰分析を実際にご自身でやったことのある方はイメージがつきやすいと思いますが、オッズ比を算出する際に95%信頼区間、p値も算出されているかと思います。これは「オッズ比=1(関連がない)」という帰無仮説を検定していることになります。そのため、関連が統計学的に有意であるのかそうでないのかをたやすく理解することができます。
重要!オッズ比を解釈する際の注意点
オッズ比は便利で汎用されているがために、間違った解釈もされていることがあります。以下の点を押さえて、正しく解釈できるようにしましょう。

冒頭でも述べましたが、①が一番勘違いされやすいポイントです。特にアウトカムの発症率10%以上の場合はリスク比との差が大きくなるため、注意しましょう。
②、③はご自身で解析をしたことがあれば、実感があるかもしれません。投入する共変量(年齢、性別など)を変えることで、曝露のオッズ比も影響を受けて変化します。そのため、異なるモデル内の曝露を比較することはできません。
例)アウトカム:心血管疾患の発症
モデルA:性別、年齢、糖尿病、高血圧(曝露)
モデルB:性別、年齢、学歴、高血圧(曝露)
この場合、モデルAとモデルBの高血圧のオッズ比を比較することはできません。
また、集団の構成が異なる他の研究と比較することもできません。
間違った解釈)「我々の研究では高血圧の心血管疾患に対するオッズ比は3.0であった。これはヨーロッパ人を対象とした先行研究のオッズ比1.5よりも高く、日本人おいて高血圧はよりリスクとなる。」
対象集団の構成が異なり、異なるモデルを使っていることが多く、他の研究のオッズ比と比較してはいけません。ではどのように解釈するのがよいでしょうか。
正しい解釈)「我々の研究では高血圧の心血管疾患に対するオッズ比は3.0であり、ヨーロッパ人を対象とした先行研究のオッズ比1.5と報告されている。人種にかかわらず、高血圧は心血管疾患のリスクであると言える。」
このように関連の大小は述べられませんが、方向性が同じであるということは言えます。
計算しやすいがゆえに汎用されているオッズ比、正しく解釈しましょう!


コメント