2つの連続変数の関連をみる場合、相関、回帰の2つがあります。
ある集団の身長と体重の関連を例に挙げてみます。
相関
身長と体重をプロットした散布図は図1のようになります。
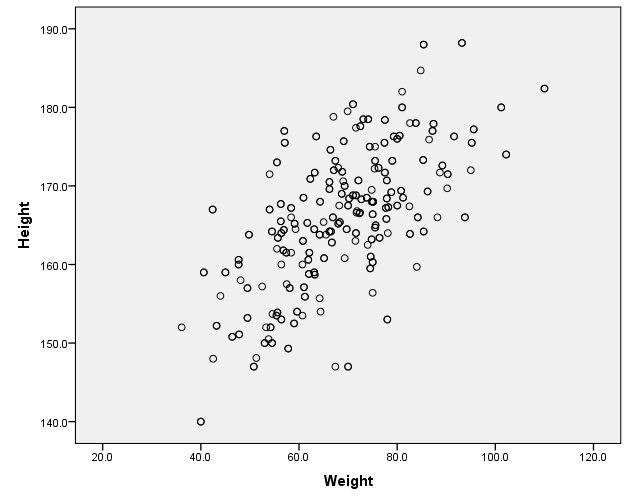
この2つの変数の関連性の強さを表すものが「相関」です。一方が増えるともう一方が増える場合に正の相関、一方が減るともう一方が減る場合には負の相関があると言えます。相関の強さを表す係数としてr=相関係数があります。相関係数は-1~1の値をとります。
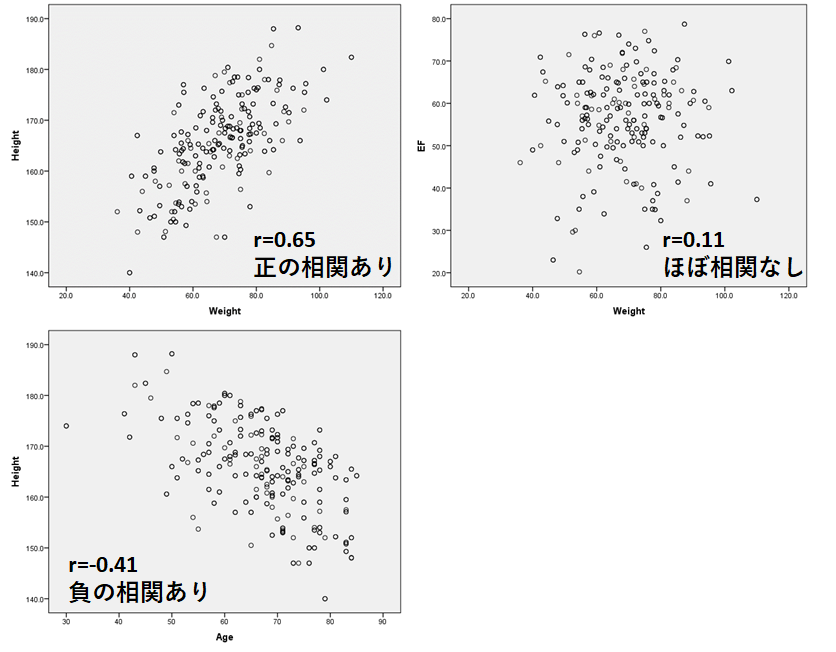
有意な相関があるかどうかの検定はPearsonの相関係数、Spearmanの順位相関係数があります。2つの連続変数が両方とも正規分布に従う場合にはパラメトリック検定であるPearsonの相関係数、それ以外の場合はノンパラメトリック検定であるSpearmanの順位相関係数を用います。
一般的には
r=0 相関なし
0<|r|<0.2 ほとんど相関はない
0.2<|r|<0.4 弱い相関あり
0.4<|r|<0.7 相関あり
0.7<|r|<1 強い相関あり
とされています。
また、有意な相関であるかどうかを示す有意確率も算出されます。有意確率は帰無仮説「2つの連続変数には相関がない、r=0」を検定しています。注意すべきは、このときにp値は相関の強さをみるものではないということです。そのため、わずかでも関連があればp<0.05となります。そのため、相関の強さは必ず相関係数を確認しましょう。
回帰
2つの連続変数の関連をみるという意味では相関と同じですが、回帰では変数yを変数xで説明(予測)できるかの試みを行っており、回帰式で2つの変数の関連をみます。回帰式が直線となる直線回帰が基本となりますが、曲線回帰という方法もあります。ここでは直線回帰の考え方を説明していきます。
直線回帰の考え方
図1のような散布図からyを予測する式を作るのが回帰式です。回帰式y=ax+bの係数aと定数bを算出します。ここではyが従属変数(目的変数)、xが独立変数(説明変数)です。
この例では従属変数を身長、独立変数を体重とします。
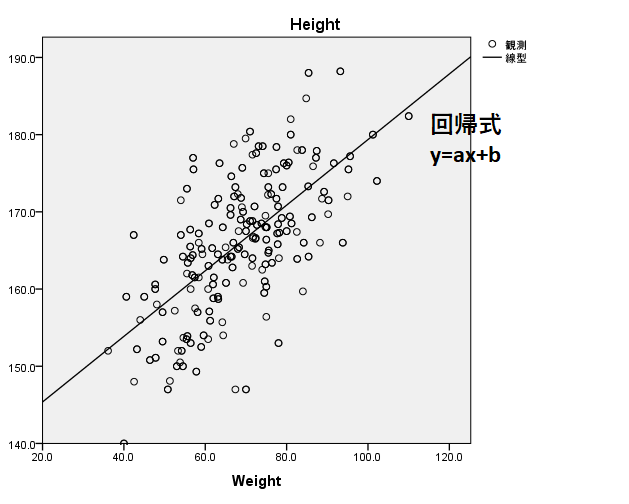
回帰式は最小二乗法の原理をもとに算出されます。
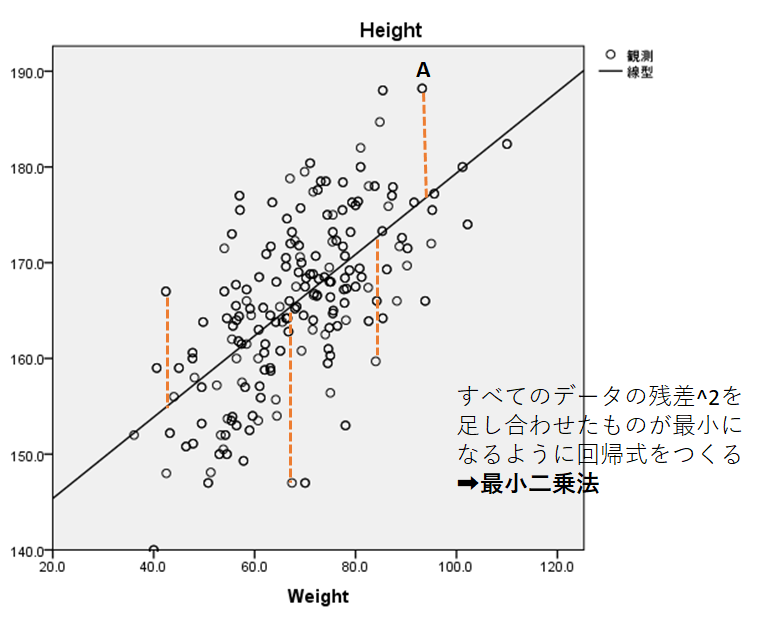
図4ではたくさんの点が実測のデータ、線が回帰式(予測のデータ)です。実測のデータと予測のデータの差を残差といい、この残差が少ないほど適切な予測式であると言えます。点Aでは実測値が188、回帰式から算出した予測値が157であったとすると188-157=31で、残差31となります。残差は正、負両方の値があるのですべての点における残差の二乗をすべて足し合わせた数(平方和)が最も小さくなるように回帰式をつくります。
R2 決定係数
回帰式の適合度の指標として、R2 決定係数があります。言い換えると、全体の変動のどの程度回帰式で予測できるかどうか、どれくらい優れた予測式であるかどうかを表すものです。
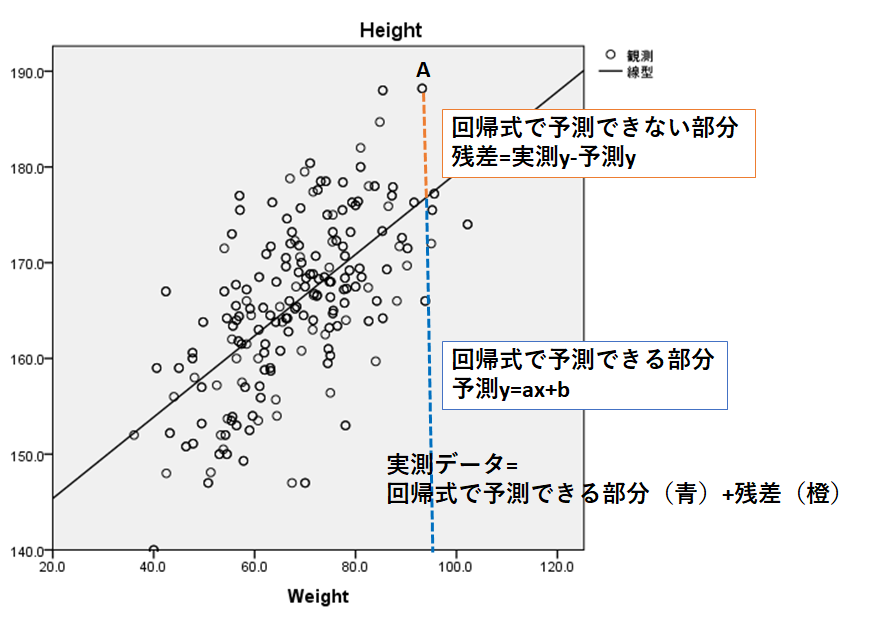
図5をみてみましょう。実測データ=予測データ+残差の関係があり、各々の実測データは回帰式で予測できる部分(回帰式)と予測できない部分(残差)に分けることができます。点Aでは青の部分が回帰式によって予測できる部分、橙色の部分が予測できない部分(残差)です。これをすべての点において行い、平方和をとります。
R2=回帰式で説明できる部分の平方和/実測データの総変動
で示されます。Rは0から1の値をとり、回帰式が全く役に立たない場合はR2=0、回帰式ですべて説明できる場合にはR2=1となります。決まりはありませんが、実際にはR≧0.7、R2≧0.5であれば有効な予測式であると言えます。


コメント