Stataで記述統計

データをまとめる際に集めたデータがどのような特徴を持っているのか知っておくことはとても重要です。データの挿入ができたら、まず一番初めに記述統計を行います。

※このページの見方※
コマンドは・に続く部分です。
黒文字➡コマンド（定型）、青文字➡連続変数（continuous variable）、赤文字➡名義変数（categorical variable）
青文字や赤文字を変えて使いましょう。

今回、例で使用する変数
Age　年齢、連続変数
HT　高血圧、名義変数　0＝なし、1＝あり
DrugA　薬剤Aの使用、名義変数　0＝なし、1＝あり

連続変数の記述統計

ここでは連続変数である“Age”の記述統計を行います。“HT”は高血圧の有無を示す名義変数です。

3パターンありますので、目的に応じて使い分けましょう。

パターン①　シンプル　平均、標準偏差、最大値、最小値

パターン②　①に加えて、パーセンタイル、尖度、歪度

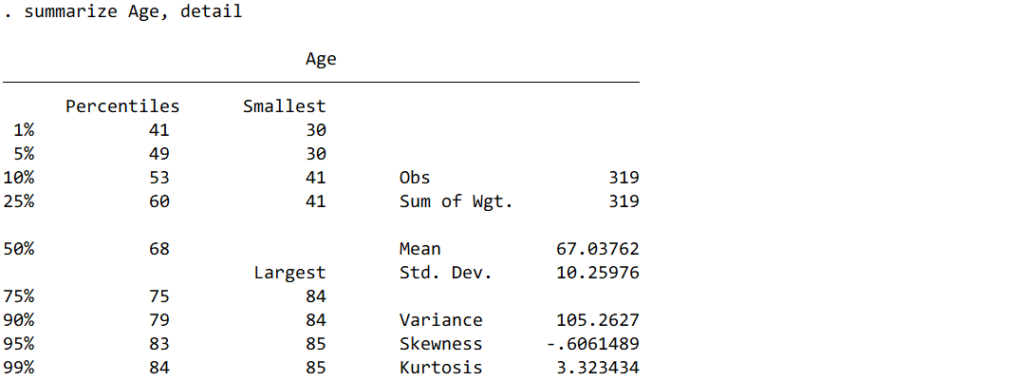
パターン③　カテゴリー変数ごとに見たい場合。パターン②のように後ろに“, detail”をつけるとパターン②のように詳細に出力されます。

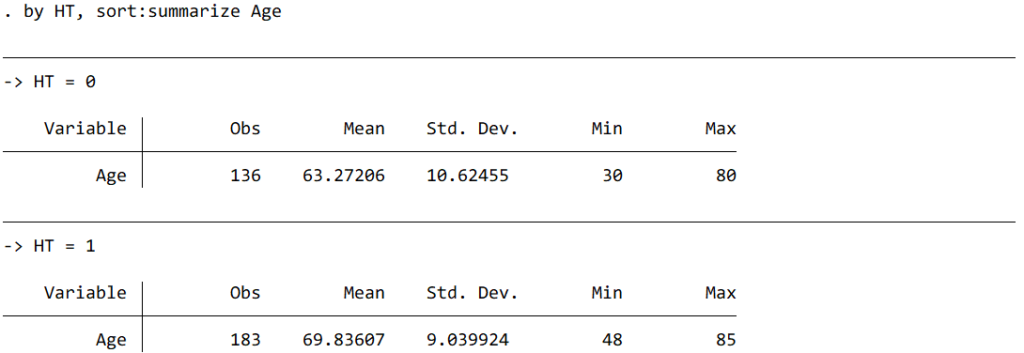
決まり事として論文や学会で報告する場合は
正規分布に従う場合：平均±標準偏差　Age 67.0±10.3
正規分布に従わない場合：中央値（25パーセンタイル-75パーセンタイル） Age 68 (60-75)
というように記載します。

名義変数の記述統計

名義変数である“HT”の記述統計を行います。

パターン①　カテゴリーごとの数とパーセンテージが表示されます。

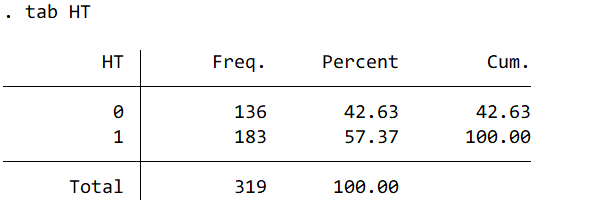
パターン②　2つのカテゴリーで2×2テーブルを作ります。“, col row”は行と列のパーセンテージを出力してね、ということですので、不要であれば片方だけ、もしくはなくてもOKです。

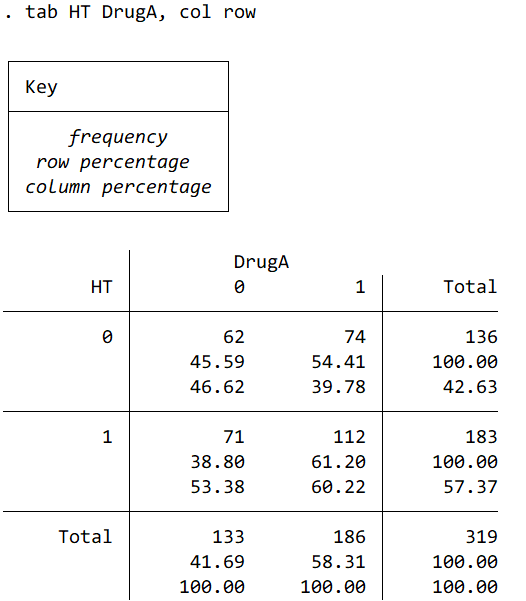
報告するときは 度数（%）で報告します。 HT 183 (57.4%)