正規分布とは?
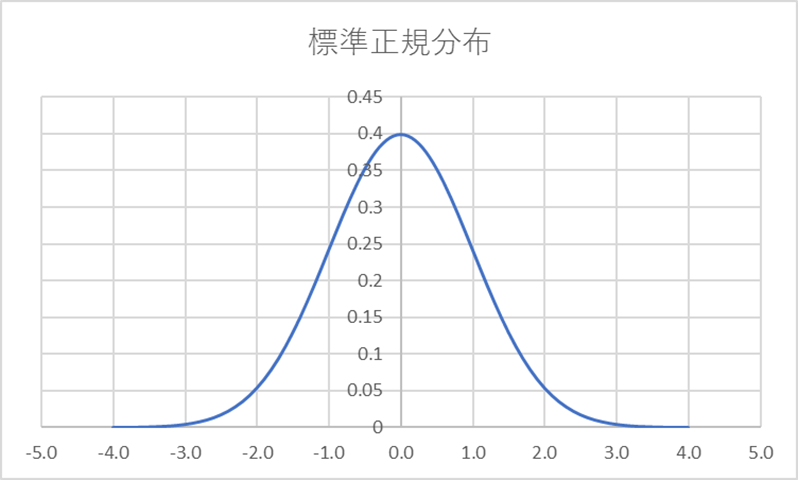
正規分布というと、統計があまり得意でない人もこのような釣り鐘型のグラフを思い浮かべることができるのではないでしょうか?これはとる値をx軸、度数をy軸に取ったものです。平均的な値に多くが分布しており、平均から離れるにしたがって少なくなります。自然界のありとあらゆるものがこのような分布で成り立っています。
実は統計でとっても大事な分布です。検定のときに出てきますが、正規分布を取るか否かによって使う統計の方法が変わってきます。まずはこの形を頭に入れておいていればOKです。
平均0、分散1の標準正規分布
正規分布の中でも、平均が0、分散が1の正規分布を標準正規分布といいます(図1)。
分散は平均との差の2乗を足し合わせたもので、どれだけばらついているかがわかります。
平均=μ(ミュー)
分散=σ2(シグマ)
標準偏差=σ
で表されます。
正規分布では平均と分散がわかればどのような分布になっているのかがわかります。
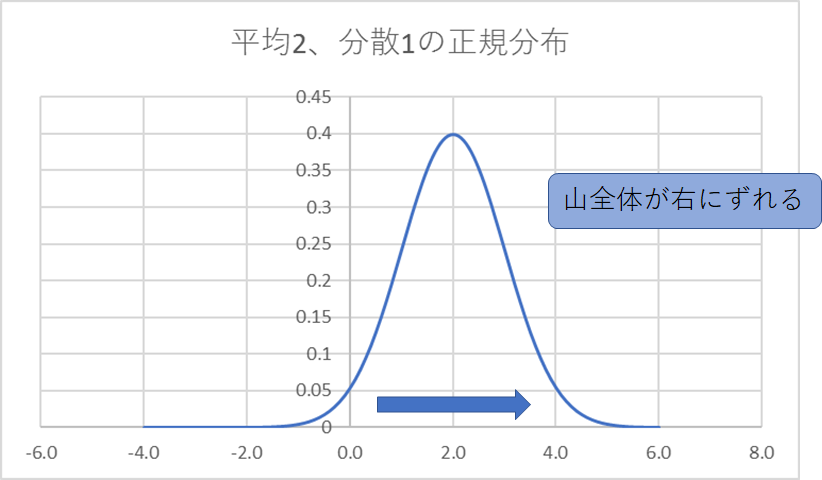
平均2、分散1の場合は標準正規分布から全体が右にずれた分布となります。
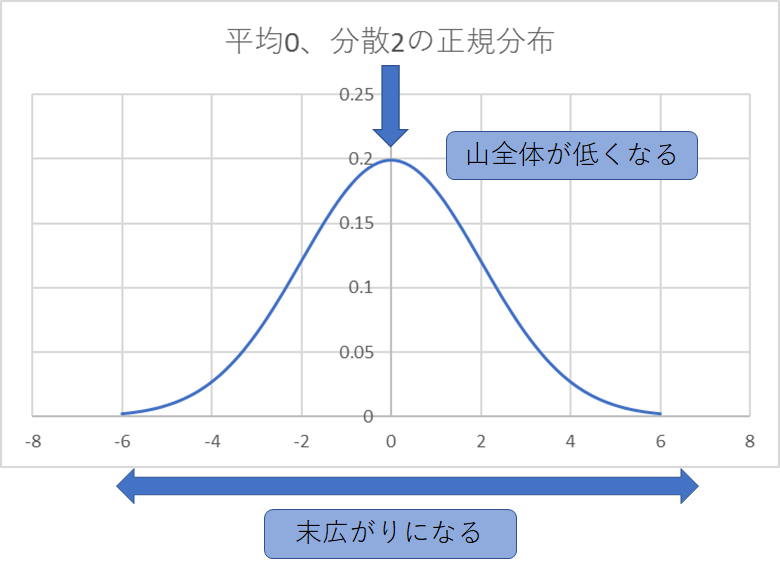
平均0、分散2の場合は標準正規分布と比較して山が低く、末広がりの分布となります。
標準正規分布が基準となるため、正規分布に従う分布は標準化という変形をして標準正規分布に見立てることで検定に用いています。
もう一つ大事なことは平均±標準偏差(μ±σ)のなかにデータ全体の68%が含まれているということです。
尖度(せんど)と歪度(わいど)
標準正規分布からどれくらい離れているかの指標として、尖度と歪度があります。
尖度は山のとんがりぐらい、歪度は山の頂点が中央からどれくらいずれているかを示します。
尖度0が基本で正の値をとると山がとんがっている、負の値をとると低くなだらかな山です。歪度も0が基本で正の値をとると左にずれた山(山の右側が広い)、負の値をとると右にずれた山(山の左側が広い)となります。
つまり図2では歪度<0、図3では尖度<0ということになります。
尖度、歪度も検定の際に正規分布しているかどうかの指標になりますので、覚えておきましょう。
今日のポイント
①釣り鐘型の正規分布
②平均±標準偏差(μ±σ)のなかにデータ全体の68%が含まれている


コメント