従属変数、独立変数が両方とも名義変数の場合、χ2検定を行います。χ2検定は独立の検定とも呼ばれます。
χ2検定の基礎知識についてはこちら>>X2(カイ二乗)検定の基礎知識
検定方法の選択についてはこちら>>検定方法 いつ何を使う?
※このページの見方
コマンドは・に続く部分です。
黒文字➡コマンド(定型)、青文字➡連続変数(continuous variable)、赤文字➡名義変数(categorical variable)
青文字や赤文字を変えて使いましょう。
今回、例で使用する変数
DrugA 薬剤Aの使用、名義変数 0=なし、1=あり
ad2 再入院、名義変数 0=なし、1=あり
stroke 脳梗塞の既往、名義変数 0=なし、1=あり
χ2検定
従属変数:再入院(ad2)、独立変数:Drug Aの使用(Drug A)としています。DrugAの使用の有無によって再入院率に差があるかを検定してみましょう。

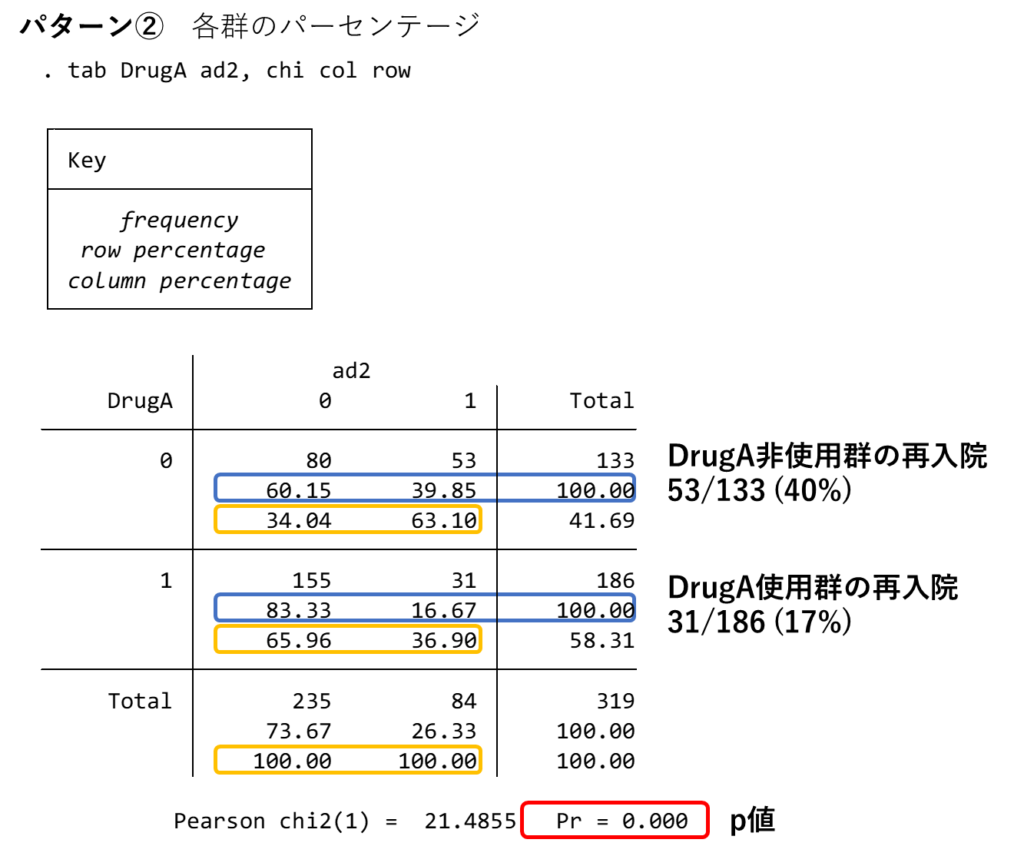
パターン②では各群のパーセンテージが算出されますので、こちらのほうがおすすめです。colが横のパーセンテージ(青色)、rowが縦のパーセンテージ(黄色)を示しており、片方だけでも算出されます。
この場合はDrugA非使用群では再入院が53/133 (40%), DrugA使用群では31/186 (17%)でDrugA使用群で再入院率が少ないという結果ですが、これは有意な結果でしょうか。
ここでχ2検定の結果をみてみると、p<0.01となっており、この差は有意な差であると言えます。
Fisherの正確検定
通常は従属変数も独立変数も名義変数の場合はχ2検定を行いますが、全サンプル数が20未満、少なくとも1つのセルの期待度数が5未満の場合にはFisherの正確検定を使います。
X2検定とFisherの正確検定の使い分けについてはこちら>>X2(カイ二乗)検定の基礎知識
別の例を挙げてみます。従属変数:脳梗塞の既往(stroke)、独立変数:Drug Aの使用(Drug A)としてFisherの正確検定を行います。
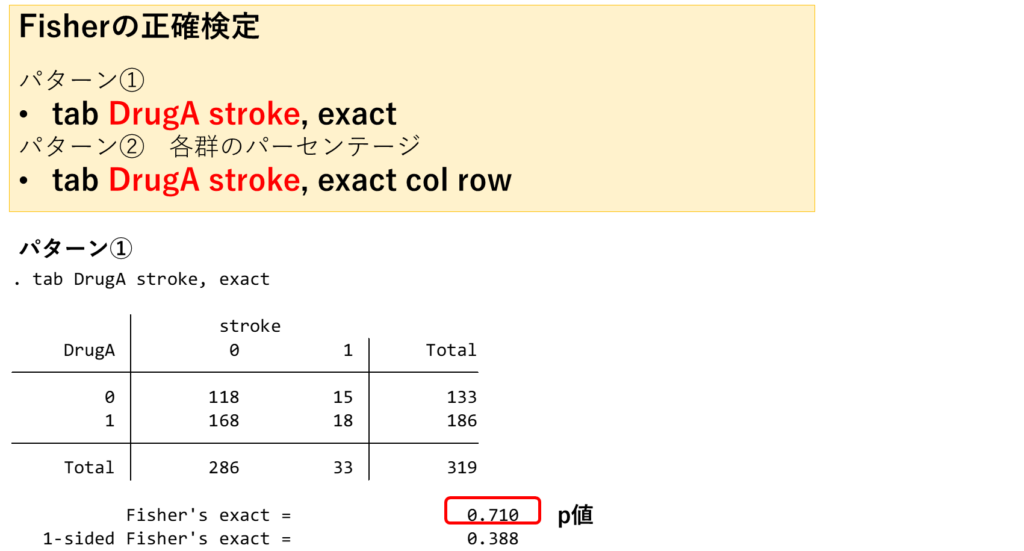

先ほどと同様に算出されます。表を見てわかるとおり、全サンプル数は319です。Fisherの正確検定でよいのか、期待値を計算してみましょう。左上(DrugA=0, stroke=0)のセルの期待値は286×133/319=119です。一番小さい期待値は右上(DrugA=0, stroke=1)のセルで期待値を計算すると、33×133/319=14となります。すべてのセルで5以上ですので、本来はχ2検定を行ってください。(いい例でなくてすみません。)
Fisher’s exactは両側検定の結果、1-sided Fisher’s exactは片側検定の結果です。通常は両側検定の結果を用います。
両側検定、片側検定についてはこちら>>両側検定と片側検定
単変量解析が終わったら多変量解析を行いましょう。
ロジスティック回帰分析はこちら>>Stataでロジスティック回帰分析



コメント