従属変数が2値数、独立変数が連続変数の場合はt検定、Mann-Whitney検定を行っていきます。独立変数が正規分布に準ずる場合はt検定、正規分布を想定できない場合はMann-Whitney検定を用います。
検定の選択についてはこちら>>検定方法 いつ何を使う?
連続変数の分布を確認する場合はこちら>>Stataで図形を描く‐ヒストグラム、箱ひげ図-
※このページの見方
コマンドは・に続く部分です。
黒文字➡コマンド(定型)、青文字➡連続変数(continuous variable)、赤文字➡名義変数(categorical variable)
青文字や赤文字を変えて使いましょう。
今回、例で使用する変数
Age 年齢、連続変数
Cr クレアチニン、連続変数
ad2 入院、名義変数 0=なし、1=あり
t検定
t検定は2群の平均に差があるかをみるために使います。
この例では再入院の有無の2群で年齢に差があるかを検定します。従属変数:再入院(ad2)、独立変数:年齢(Age)

両群のAgeの平均、標準偏差、p値などが算出されます。
Mann-Whitney検定
正規分布が仮定できない場合はノンパラメトリック検定であるMann-Whitney検定を行います。
この例では従属変数:再入院(ad2)、独立変数:Crとしています。
正規性の検定を行う
正規性の検定を行います。「正規分布している」が帰無仮説です。

p<0.05で正規分布でないと判断します。実際には正規分布しているかどうかはヒストグラムも合わせて判断します。
Mann-Whitney検定
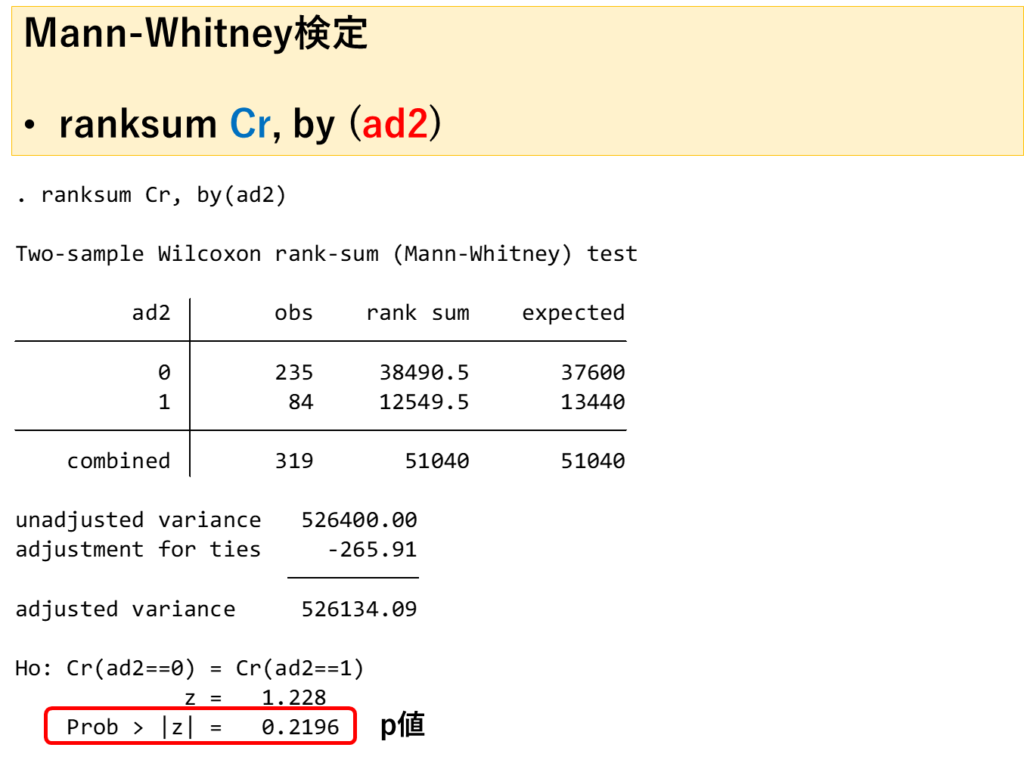
群ごとの記述統計を行う
Mann-Whitney検定ではp値を算出することはできますが、両者の中央値やパーセンタイルは算出されません。正規分布に従わない連続変数の場合は中央値、パーセンタイルを報告しなければならないため、記述統計を用いて算出します。


記述統計のときと同様、結果を記載するときは正規分布する場合は平均値±標準偏差、しない場合は中央値(25パーセンタイルー75パーセンタイル)で報告します。
単変量解析が終わったら、多変量解析を行いましょう。
ロジスティック回帰分析はこちら>>Stataでロジスティック回帰分析



コメント