2つの連続変数の関連を見たい場合には相関をみます。
相関、回帰の基礎知識についてはこちら>>相関と回帰の基礎知識
散布図を描く
まずは散布図を描きます。
例では血液検査のBNPの値と心エコーでのEF(心拍出率)の相関をみていきます。
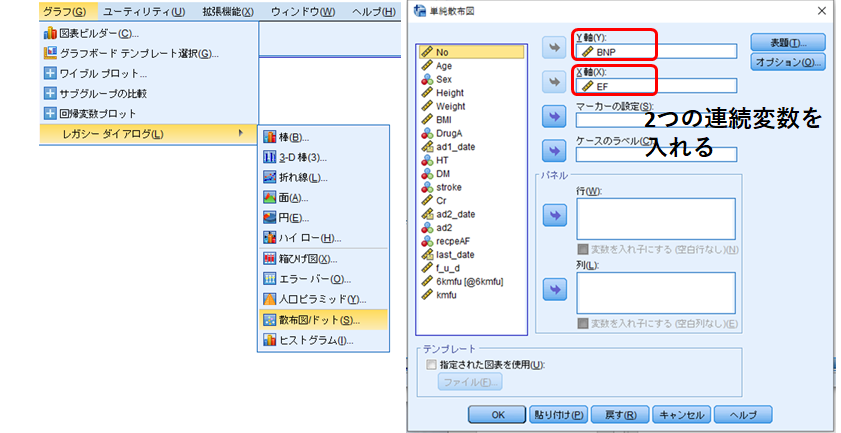
グラフ➡レガシーダイアログ➡散布図/ドット
[単純な散布]を選択します。
X軸とY軸にそれぞれ連続変数を入れて[OK]をクリック。
散布図が描けました。
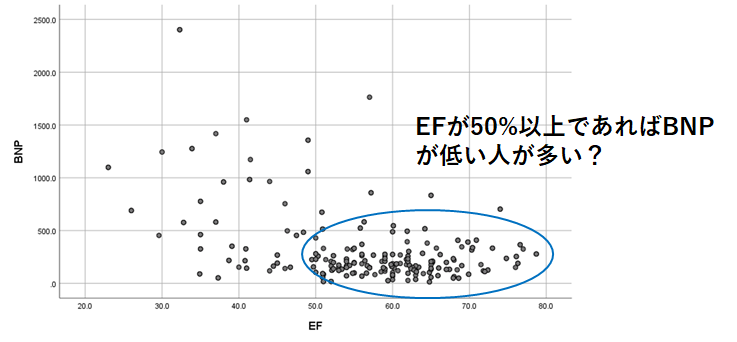
見た目にはEFが50%以上であればBNPが低い人が多そうです。
有意な関連があるかどうか、検定を行っていきます。
相関係数を算出する
分析➡相関➡2変量
変数に2つの連続変数をいれます。ここで両方とも正規分布に従っている場合は[Pearson]にチェック、少なくとも片方が正規分布でないときは[Spearman]を選択します。
この場合はEFは正規分布に従いますが、BNPは正規分布に従わないため、[Spearman]を選択しました。
正規分布しているかの確認はこちら>>SPSSで正規性の確認をする
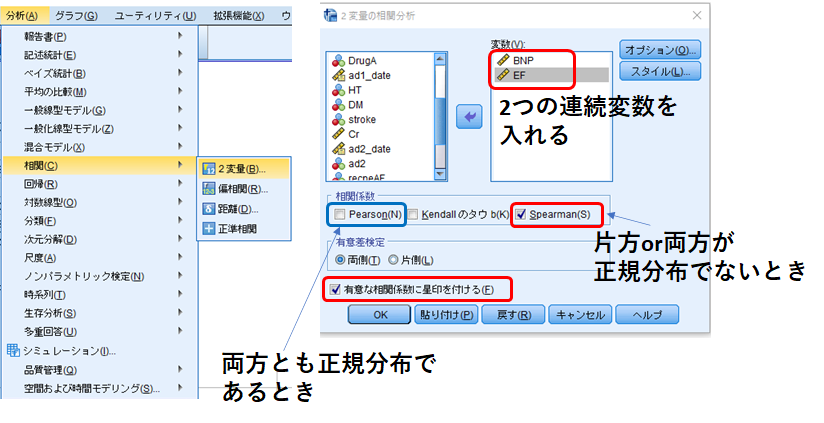
図4のように出力されました。
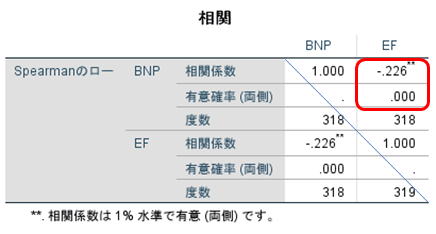
相関係数 r=-0.226、p<0.01です。
互いに独立している(つまり相関係数=0)が帰無仮説であり、p<0.05は相関係数≠0ということを示しているだけです。相関の強さは相関係数rでみます。rは-1から1の値をとり、負の値であれば負の相関(どちらか一方が大きくなると、もう片方が小さくなる)、正の値であれば正の相関(どちらか一方が大きくなると、もう片方も大きくなる)を意味します。
一般的には
r=0 相関なし
0<|r|<0.2 ほとんど相関はない
0.2<|r|<0.4 弱い相関あり
0.4<|r|<0.7 相関あり
0.7<|r|<1 強い相関あり
とされています。
この例では弱い正の相関がある、ということが言えます。
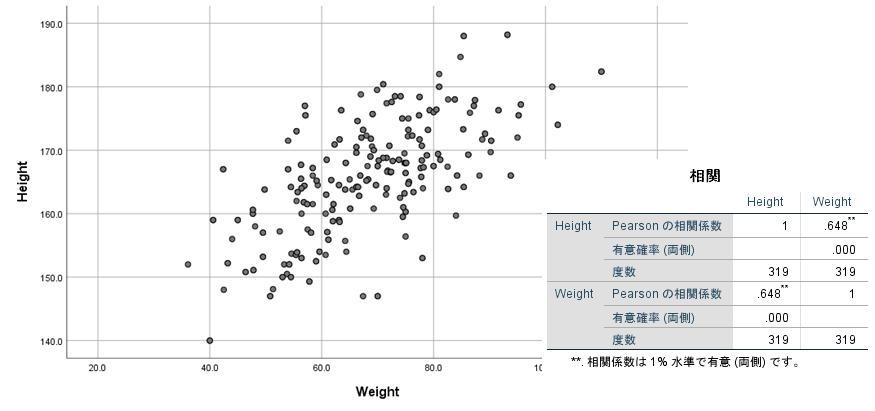
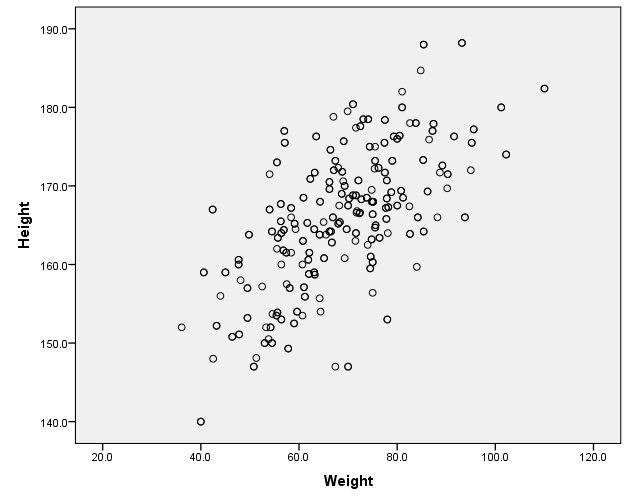
別の例として身長、体重の相関をみるとこのようになります。r=0.648で正の相関がみられます。
相関は多変量解析で独立変数を選択する際に共線性がないかどうかを確認するためにも用いられます。


コメント