SPSSでロジスティック回帰分析

単変量解析が終わったら、多変量解析を行いましょう。
多変量解析のなかでもロジスティック回帰分析は臨床研究ではとても使いやすい分析方法です。
条件は「従属変数が2値数であること」だけです。独立変数は名義変数でも、連続変数でも可能です。
従属変数が連続変数の場合は重回帰分析を行います。
重回帰分析はこちら>>SPSSで重回帰分析

独立変数の選び方

まずは独立変数の選び方です。一般的に臨床研究の場合はこのようなことが言われています。
一番上は少しわかりづらいかもしれませんが、例えば疾患発症の有無をアウトカムとしたとき、N=100の研究で発症が30人（アウトカムあり/なしの少ない方の群の数）であった場合、30/7-10＝3-4個の変数を入れてよいことになります。
年齢と性別は入れることがお作法になっていることが多いので、それを入れると残り入れられる変数は2つほどです。

SPSSでロジスティック回帰分析

それでは実際にやってみましょう。

心不全の新しい治療薬 Drug Aは心不全再入院減少に寄与するかどうかというクリニカルクエスチョンです。

分析➡回帰➡二項ロジスティック

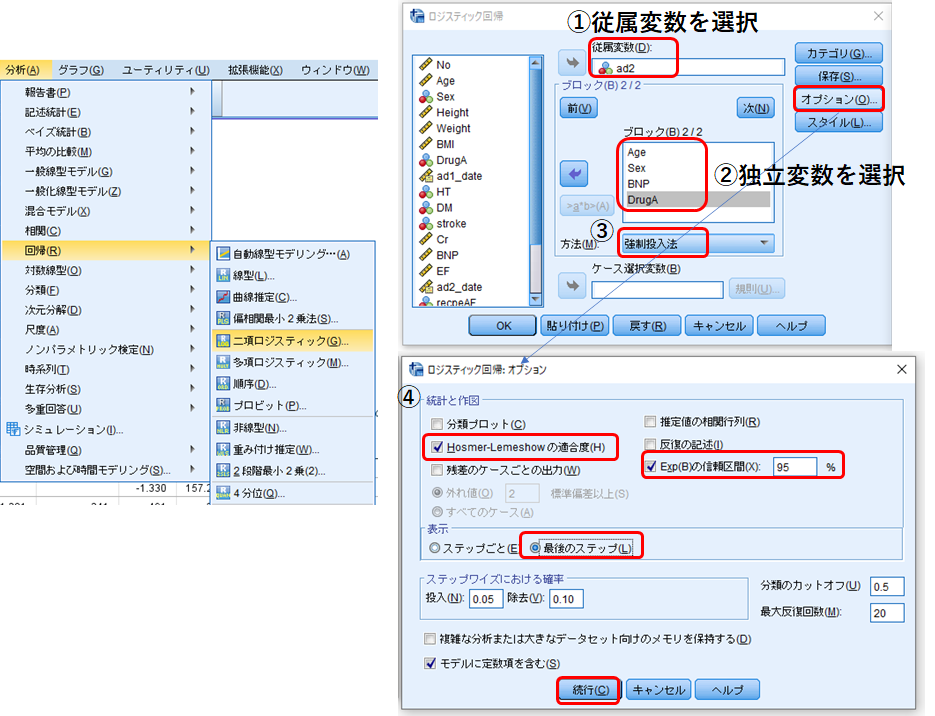
①②従属変数と独立変数をそれぞれ選択

③方法は必ず[強制投入法]を選びます。ステップワイズ法というものもありますが、これはp値によって自動的によりよいモデルを構築していくものであり、臨床研究にはあまり適さないとされています。臨床研究の場合には臨床的意義やこれまでの研究を考慮して因子を選ぶ必要があるからです。

④[Hosmer-Lemeshowの適合度]、[Exp(B)信頼区間95%]、[最後のステップ]を選択して、[続行]。

ロジスティック回帰分析　結果の解釈

図3のように出力されます。

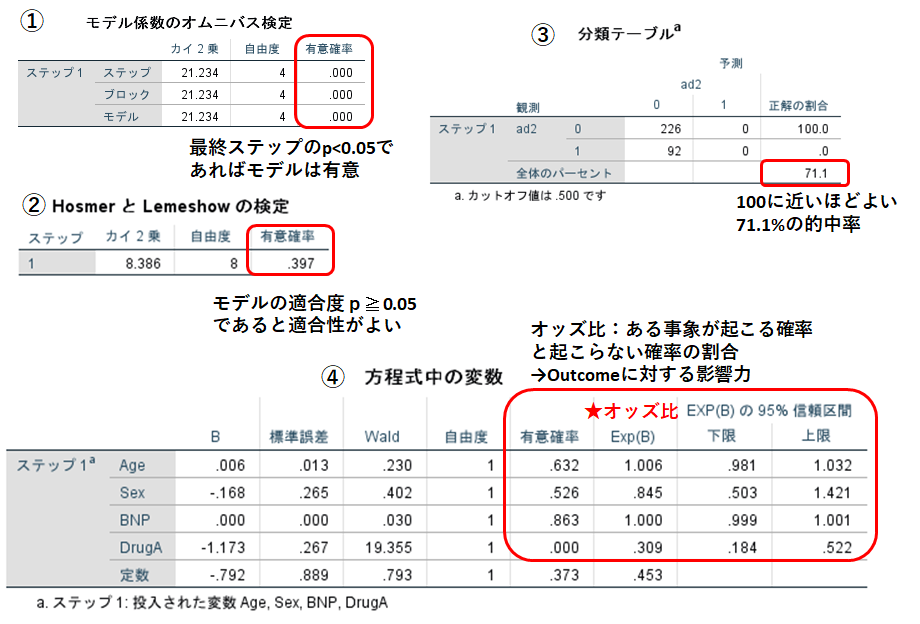
①モデル係数のオムニバス検定では最終ステップの有意確率を確認します。ここでp<0.05となればモデルの有意性あり、と評価できます。

②HosmerとLemeshowの検定ではp≧0.05であるとモデルの適合性がよいとされています。

③分類テーブルの全体のパーセントではこのモデルの的中率を示しています。ここでは的中率71.1%です。

これらのモデルの適合性の検討は新たなスコアリングシステムを作ったり、モデルを構築したりする場合には必要であると思います。しかし、強制投入法で独立変数を挿入し、ある独立変数の従属変数に対する影響の度合いを見たい場合には気にする必要はないでしょう。目的に応じて使い分けてください。

④ここではExp(B)はオッズ比、ある事象が起こる確率と起こらない確率の割合の比です。1より大きいほど、または小さいほど（比なのでマイナスにはならない）、従属変数への影響力が大きいと言えます。

この例では、年齢、性別、BNPで補正した場合、DrugAを使用すると再入院が有意に少なかったと解釈できそうです。報告する場合には、オッズ比、95%信頼区間、有意確率を記載します。

以下は詳しく知りたい人向け。読み飛ばしてもOKです。

[B]の項目はモデル式の係数です。予測式はscore=0.06×年齢-0.168×性別-0×BNP-1.173×DrugA-0.792(定数)を計算し、確率p=1/(1+exp(-1×score))で各症例の確率pが求められます。確率pは0.5を境にしてp>0.5であれば従属変数1（ここでは再入院あり）、p<0.5であれば従属変数0（ここでは再入院なし）に分類されます。この的中率が71.1%ということを示しています。この例ではBNPは係数も0、オッズ比も1であり、モデルには不要な項目であることがわかります。

〇ロジスティック回帰分析で算出されたオッズ比、正しく解釈できていますか？
>>オッズ比の解釈　－正しく解釈できていますか？－

〇ロジスティック回帰分析で作成したモデルの評価を行いたい場合はこちらを参照してください。>>SPSSでROC曲線を描く　モデルの精度を評価する

〇そもそもROC曲線って何？という方はこちらから>>ROC曲線って何？