SPSSで単回帰分析（曲線回帰分析）

2つの変数、変数yを変数xで説明（予測）するというのが回帰式です。
詳しくはこちら>>相関と回帰の基礎知識
変数yは目的変数または従属変数、変数xは説明変数または独立変数と呼ばれます。
直線的な関係がみられるときは直線回帰分析を行います。>>SPSSで単回帰分析（直線回帰分析）
直線的な関係よりも曲線的な関連の可能性が高い場合、直線回帰では精度が低い場合には曲線回帰分析を試しましょう。

単回帰分析（曲線回帰分析）

直線回帰分析のときと同様、ここでは例としてEF（心エコーでの心拍出係数）をBNP（血液検査のデータ）から予測できるか単回帰分析を行ってみます。
y（従属変数）＝EF、x（独立変数）＝BNP　です。
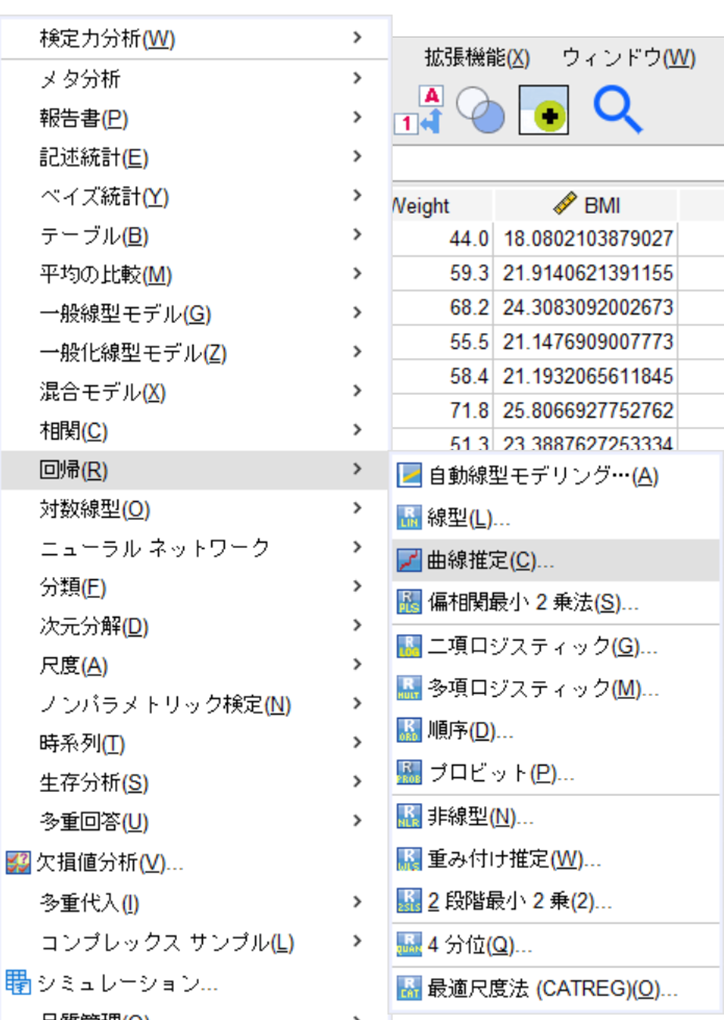
分析➡回帰➡曲線推定

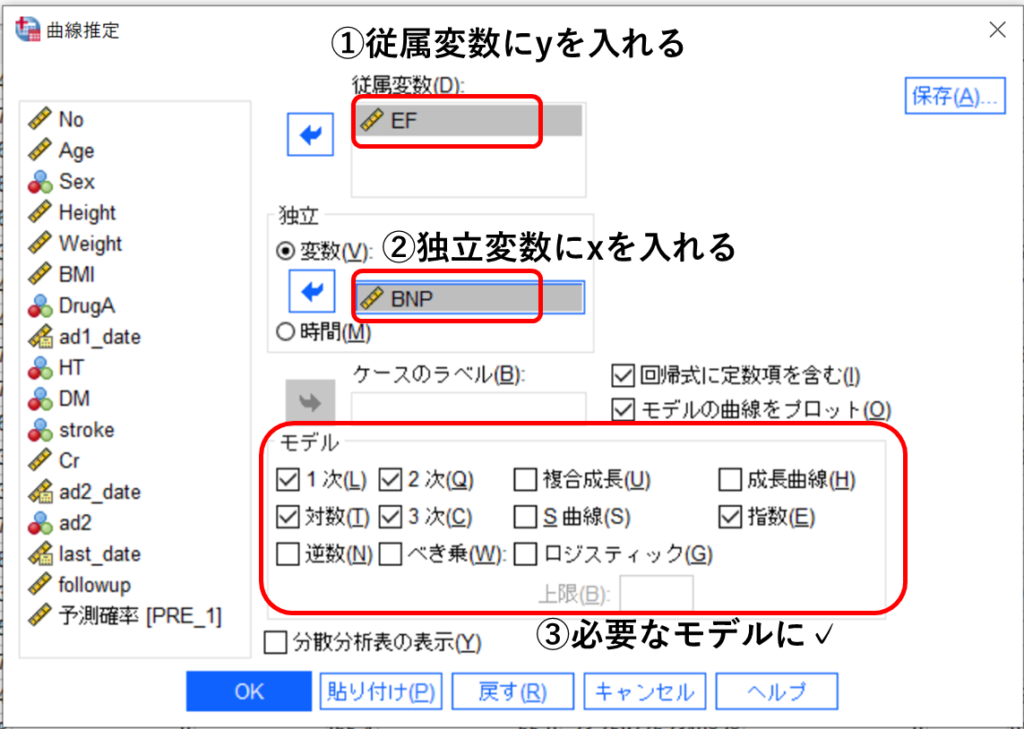
① 従属変数にy（ここではEF）を入力
② 独立変数にx（ここではBNP）を入力
③ 必要なモデルにチェックを入れる
上記を入力したら[OK]で出力されます。

結果の解釈

下記のように出力されます。

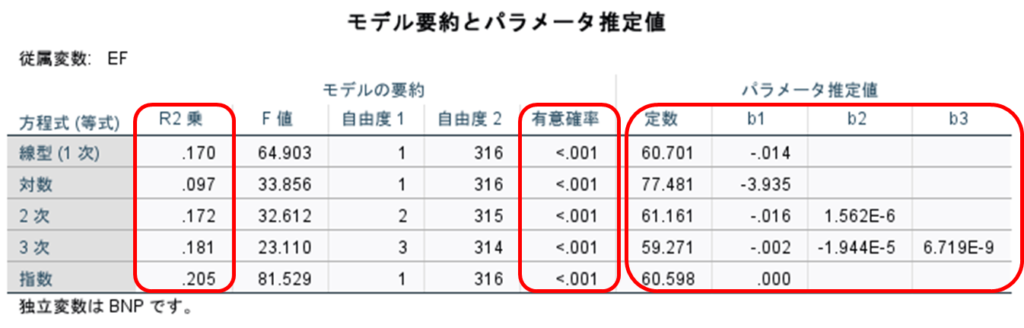
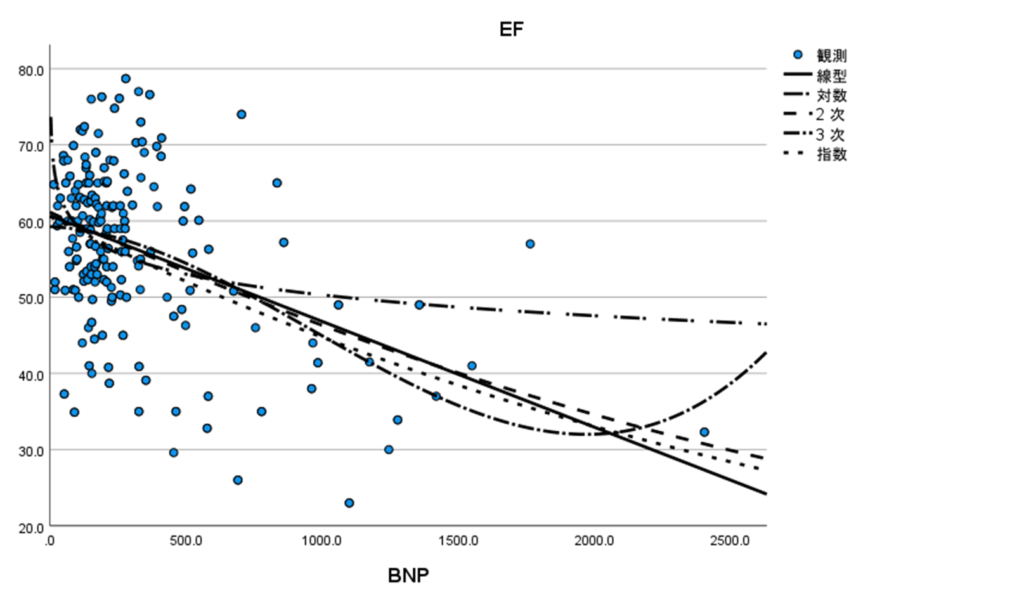
R2はすべて小さくなっているので（一般的にR2≥0.5がよいモデルとされる）ここではあまりよいモデルはできていませんが…
線形：y=60.7-0.14x
対数：y=77.5-3.94loge(x) 2次：y=61.2-0.16x+1.5610-6×2
3次：y=59.3-0.002x-1.0410-5×2+6.7210-9×3
指数：y=60.6+0.00x (小数第3位までしか表示されませんが、省略されています。0ではありません。)

ここではR2は指数関数で最も高く、この中では最も精度がよいということになります。