2つの変数、変数yを変数xで説明(予測)するというのが回帰式です。
詳しくはこちら>>相関と回帰の基礎知識
変数yは目的変数または従属変数、変数xは説明変数または独立変数と呼ばれます。
実際にSPSSで回帰分析をやってみましょう。
単回帰分析(直線回帰分析)
ここでは例としてEF(心エコーでの心拍出係数)をBNP(血液検査のデータ)から予測できるか単回帰分析を行ってみます。
y(従属変数)=EF、x(独立変数)=BNP です。
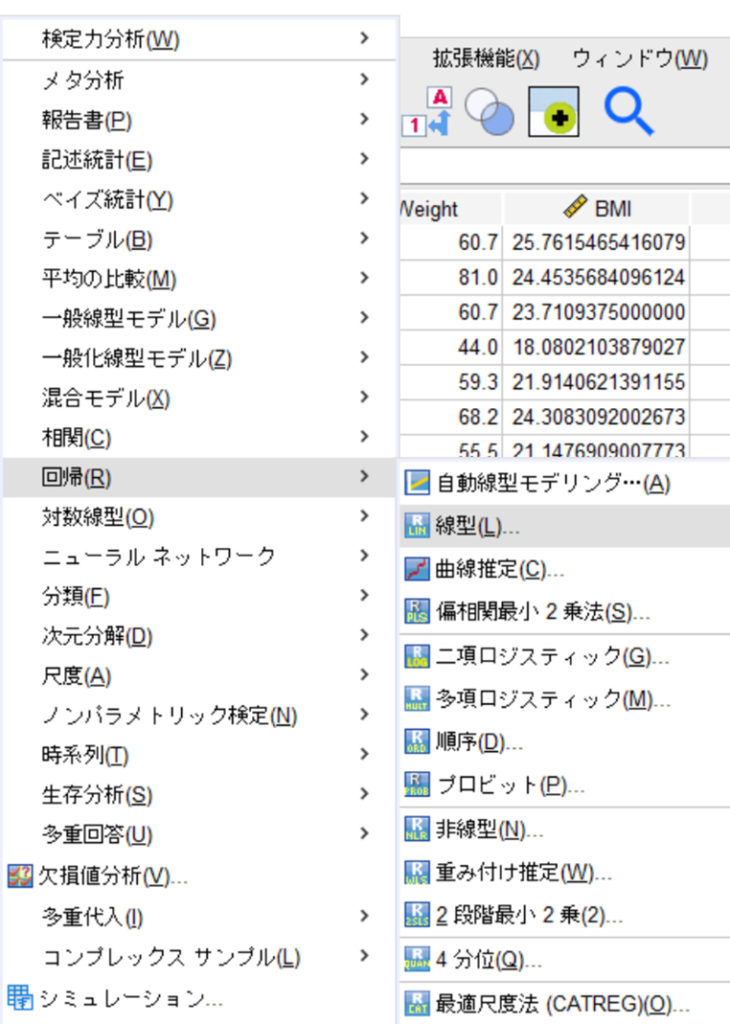
分析➡回帰➡線形回帰
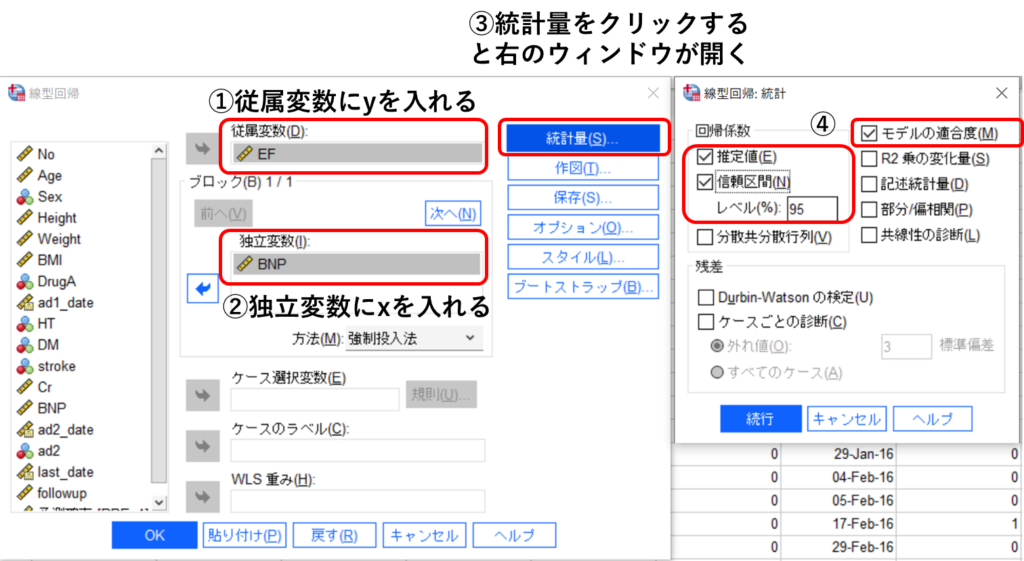
① 従属変数にy(ここではEF)を入力
② 独立変数にx(ここではBNP)を入力
③ [統計量]をクリック
④ [推定値]、[信頼区間]、[モデルの適合度]にチェックを入れる
上記を入力したら[OK]で出力されます。
結果の解釈
図3のように出力されます。
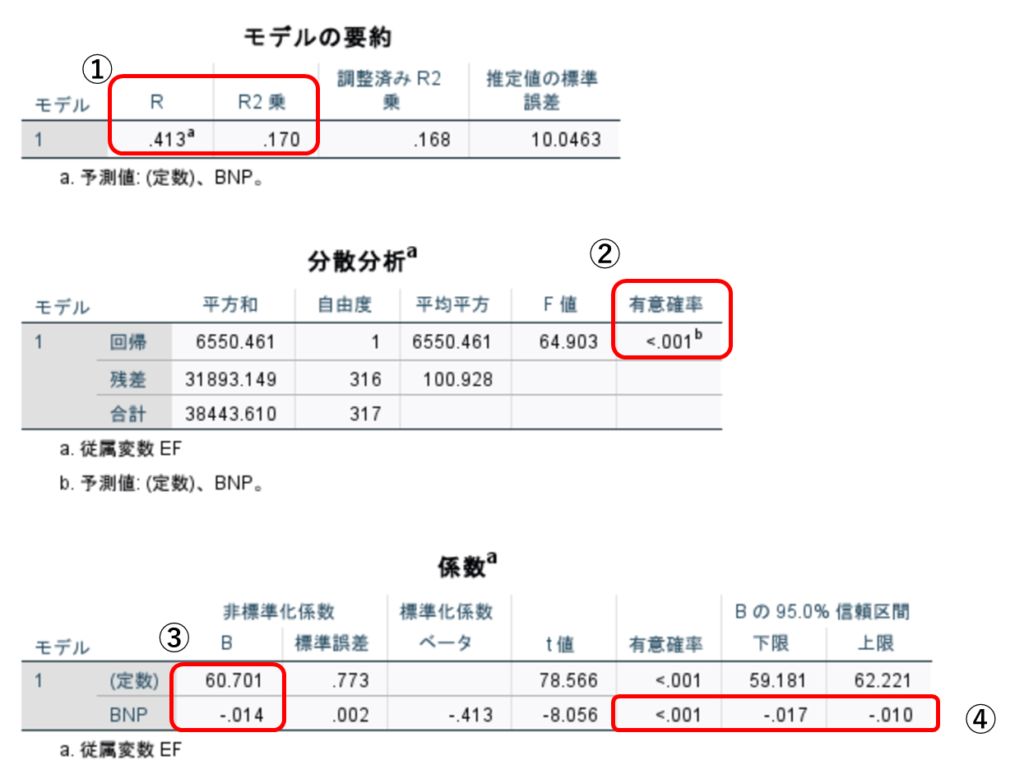
① R、R2乗値を確認。Rは0から1の値をとり、回帰式が全く役に立たない場合はR2=0、回帰式ですべて説明できる場合にはR2=1となります。決まりはありませんが、実際にはR≧0.7、R2≧0.5であれば有効な予測式であると言えます。
② p<0.05であればこの回帰式が有意であるということが言えます。
③ 回帰式の係数です。この解析からはEF=60.7-0.014×BNPという回帰式が算出されました。
④ 係数のp(有意確率)と95%信頼区間です。p<0.05であり、95%信頼区間も1をまたいでいないので、有意な回帰式であるということが言えます。
回帰式の精度が低いとき
回帰式の精度が低いときは散布図を描いてみましょう。
描き方はこちら>>SPSSで相関をみる
この例では散布図は図のようになりました。
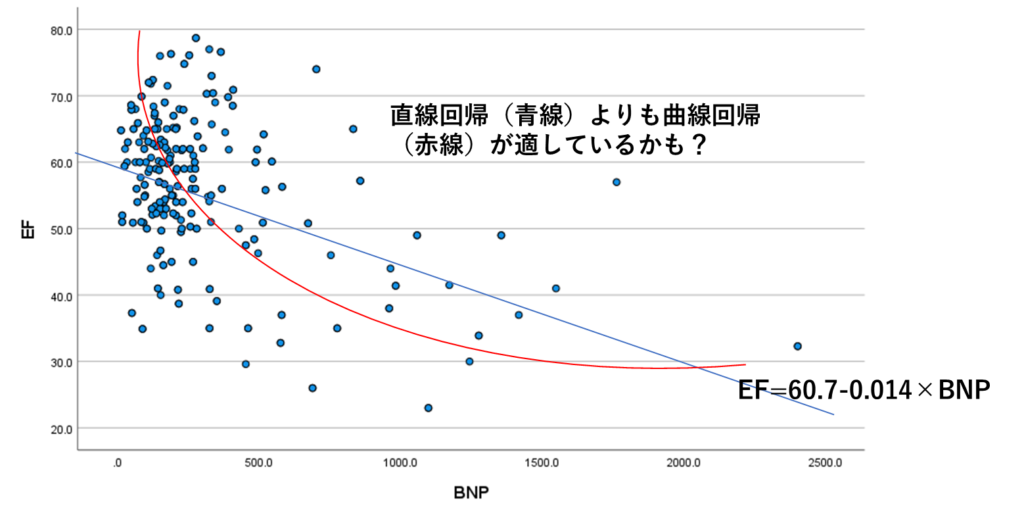
ここで行った回帰は直線回帰でしたが、曲線回帰を試してみる価値があるかもしれません。
また、回帰係数が有意なのに予測精度が低い場合は、いくつかの変数を組み合わせる重回帰分析を行うと予測精度が上がると思われます。
曲線回帰分析はこちら>>SPSSで単回帰分析(曲線回帰分析)
重回帰分析はこちら>>SPSSで重回帰分析



コメント