従属変数が2値数、独立変数が連続変数の場合はt検定、Mann-Whitney検定を行っていきます。独立変数が正規分布に準ずる場合はt検定、正規分布を想定できない場合はMann-Whitney検定を用います。
検定の選択についてはこちら>>検定方法 いつ何を使う?
正規性の検定についてはこちら>>SPSSで正規性の確認をする
t検定
t検定は2群の平均に差があるかをみるために使います。
この例では年齢と心不全再入院の関連を見てみます。従属変数:再入院(ad2)、独立変数:年齢(Age)としています。
分析➡平均の比較➡独立したサンプルのt検定
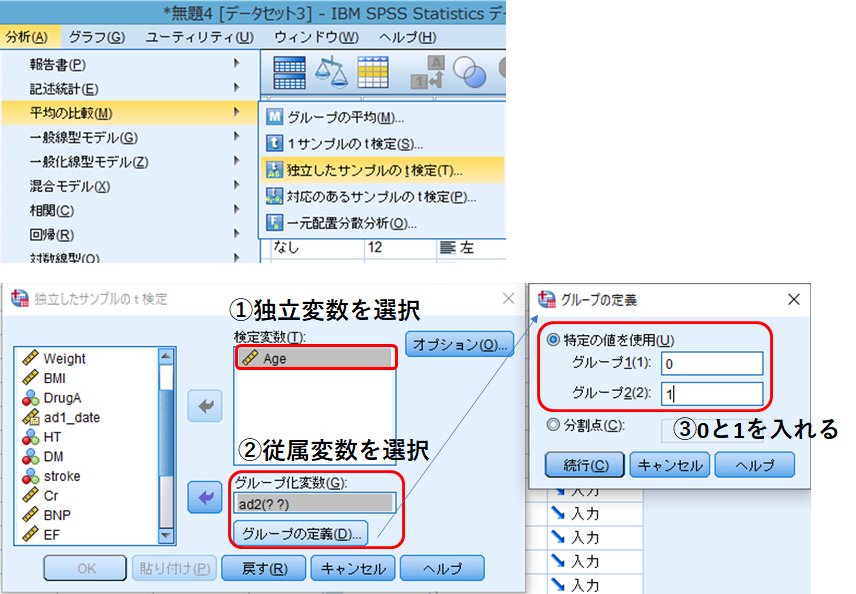
検定変数に独立変数をいれ、グループ化変数に従属変数(アウトカム)を入れます。アウトカムは2値数である必要があります。グループの定義をクリックして、それぞれ[0]、[1]と入力します。入力できたら[OK]をクリック。
すると図2のように出力されます。
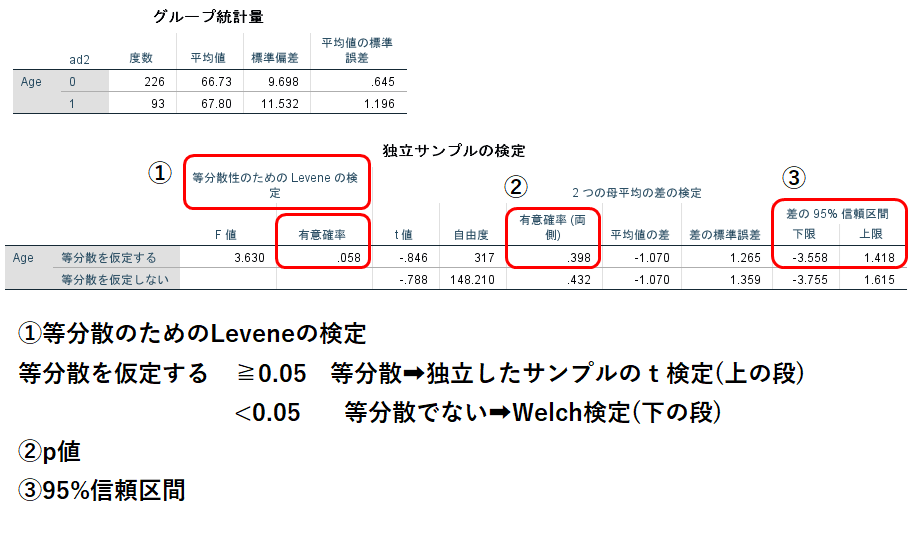
両群の平均と標準偏差を確認し、等分散性のためのLeveneの検定をチェック。有意確率が0.05以上であれば等分散しているということなので、そのまま上の段(独立したサンプルのt検定)の有意確率がp値となります。0.05未満であれば等分散でないことが仮定されるので、下の段(Welch検定)の有意確率がp値となります。95%信頼区間は0をまたいでいれば有意でない、どちらかに偏っていれば有意な差であると判断できます。
この例ではLeveneの検定ではp=0.058なので等分散と過程できますので、上の段を見ます。P=0.40 (95%信頼区間 -0.36-1.42)であり、有意な差ではないことがわかります。
Mann-Whitney検定
正規分布が仮定できない場合はノンパラメトリック検定であるMann-Whitney検定を行います。
この例では心不全再入院の有無とCrの関連を見てみます。従属変数:再入院(ad2)、独立変数:Crとしています。
Mann-Whitney検定 両群に差があるか確認する
分析➡ノンパラメトリック検定➡独立サンプル
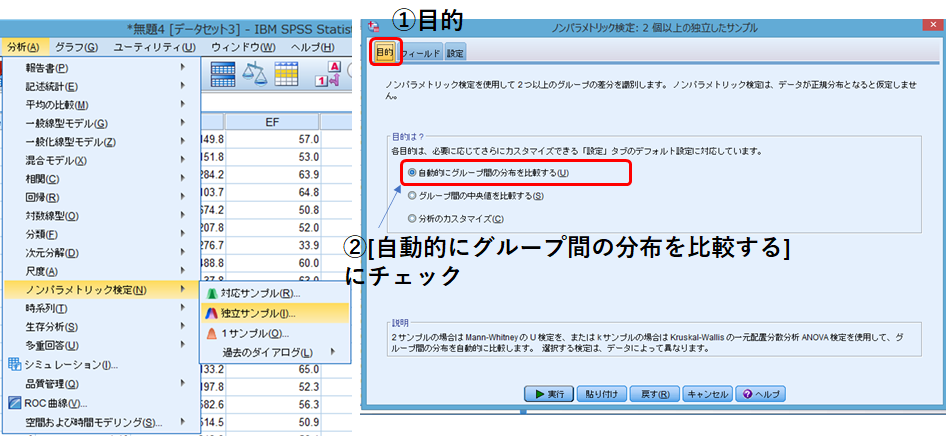
上の3つのタブを一つずつチェックしていきます。
目的:[自動的にグループ間の分布を比較する]をチェック
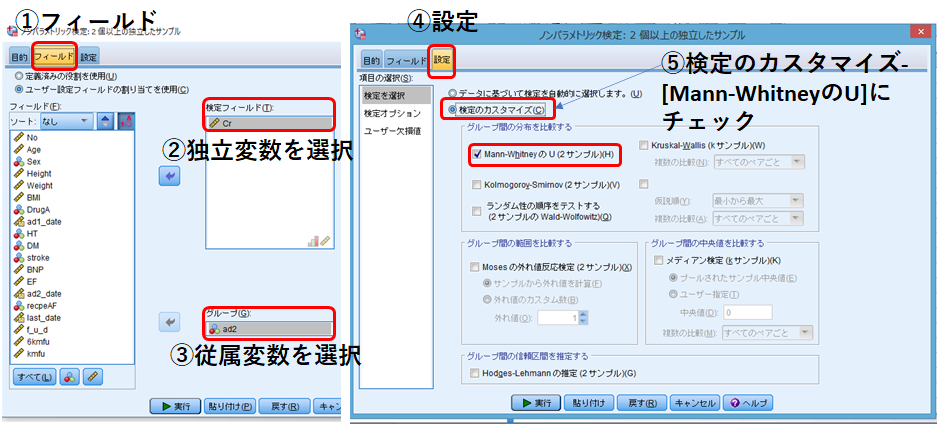
フィールド:検定フィールドには独立変数、グループには従属変数を選択
設定:[検定のカスタマイズ]、[Mann-WhitneyのU]にチェック
[実行]をクリックすると出力されます。
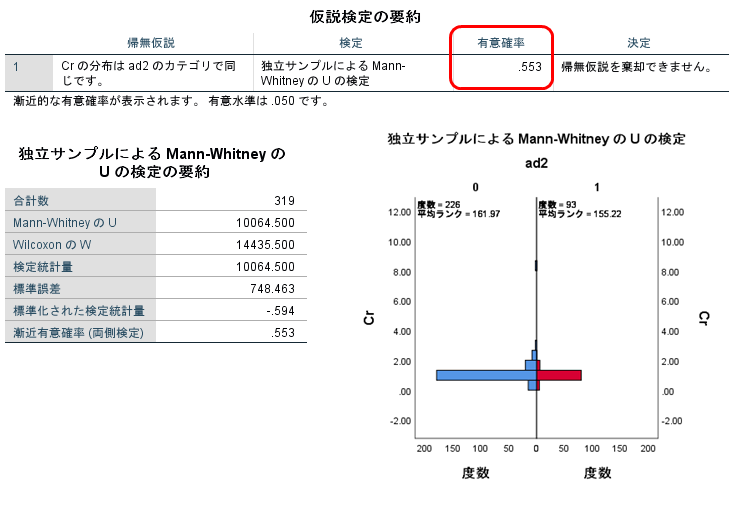
p=0.55となっており、有意ではありません。
群ごとの記述統計を行う
Mann-Whitney検定ではp値を算出することはできますが、両者の中央値やパーセンタイルは算出されません。正規分布に従わない連続変数の場合は中央値、パーセンタイルを報告しなければならないため、記述統計を用いて算出します。
分析➡記述統計➡探索的
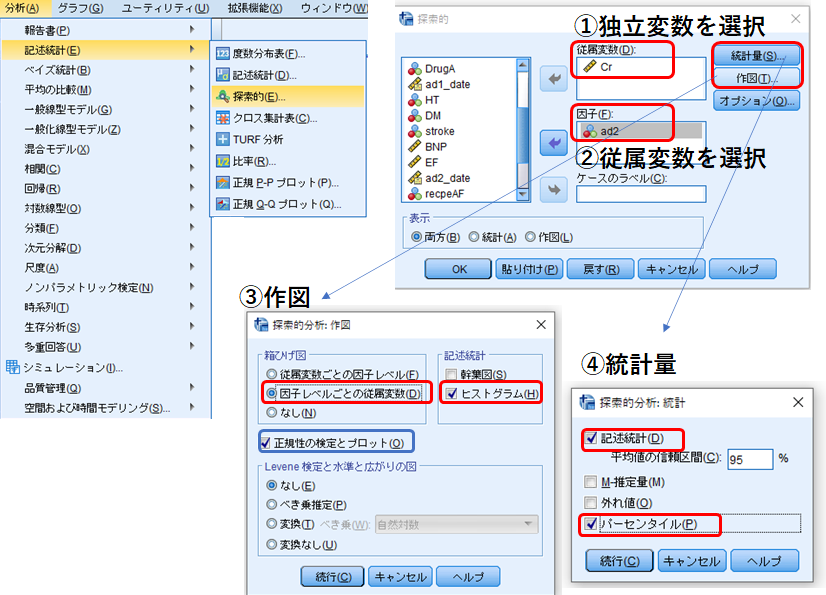
独立変数と従属変数を選択し、[作図]をクリックします。③作図では[因子レベルごとの従属変数]、[ヒストグラム]にチェック。正規性の検定が必要であれば、[正規性の検定とプロット]をチェックします。④統計量は[記述統計]、[パーセンタイル]にチェックを入れます。
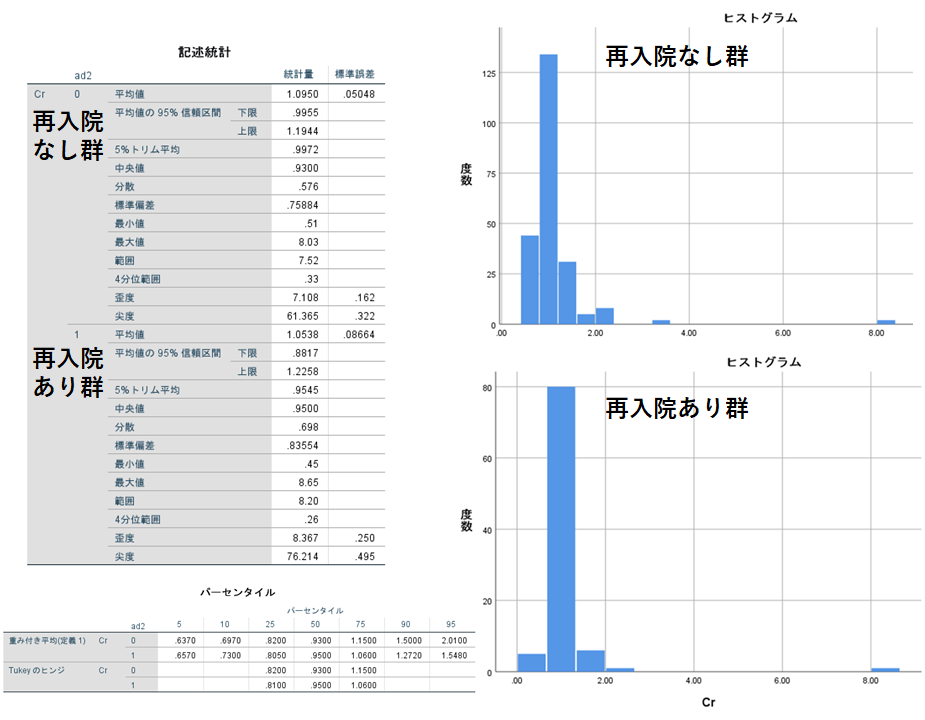
このように従属変数(ここでは再入院)の群ごとに結果とヒストグラムが表示されます。ここから中央値、25パーセンタイル、75パーセンタイルを読み取ります。
[正規性の検定]にチェックをつけた場合
正規性の検定を行った場合は検定結果とQ-Qプロットが出力されます。
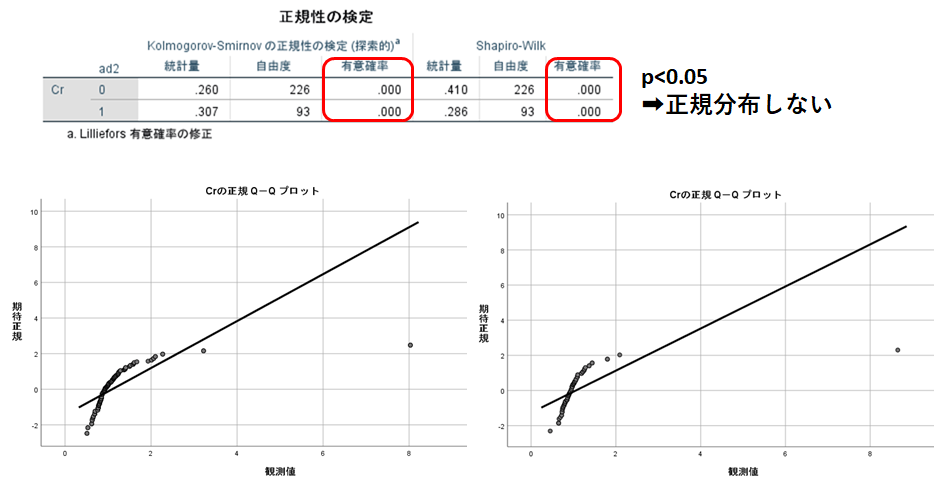
Kolmogrov-Smirnov検定、Shapiro-wilk検定、両者とも正規性の検定であり、0.05以上だと正規分布、未満であれば正規分布ではないことを示します。ただし、nが大きくなるとヒストグラムでは正規分布となっているにも関わらず、検定ではp<0.05(正規分布ではない)と表示されることがあります。必ずヒストグラムを描いて確認するようにしましょう。
Q-Qプロットは正規分布する場合は実線の直線状に点が並びます。この場合はだいぶはずれているのが分かります。
正規性の検定についてはこちら>>SPSSで正規性の確認をする
記載のしかた
記述統計のときと同様、正規分布する場合は平均値±標準偏差、しない場合は中央値(25パーセンタイルー75パーセンタイル)で報告します。


コメント