従属変数、独立変数ともに2値数の名義変数の場合、結果は2×2のクロス集計表にまとめられます。2群でアウトカムの発症に差があるかをみる場合にはX2検定やFisherの正確検定を用います。
ここではクロス集計表や独立の検定とも呼ばれるX2検定の基礎知識、Fisherの正確検定の使い方を学んでいきます。
クロス集計表でわかること
要因Aと疾患Bの発症に関連があるかをみる場合、図1のような表に結果をまとめることができ、これをクロス集計表と呼んでいます。
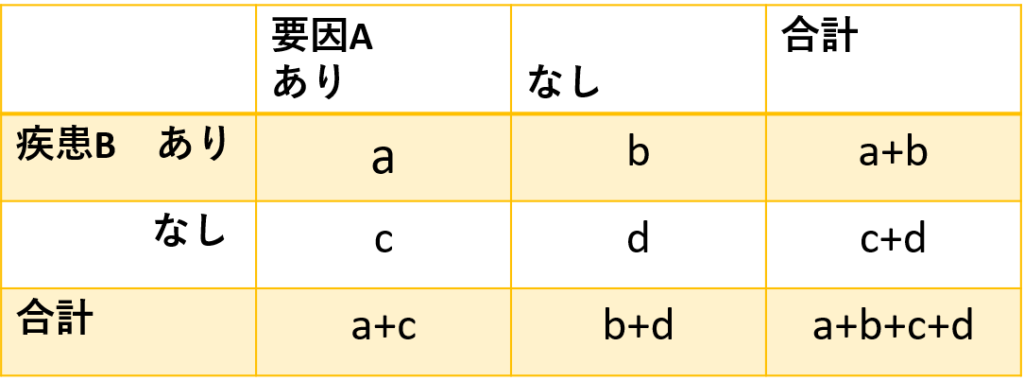
要因Aがある割合 P(A)=(a+c)/(a+b+c+d)
疾患Bを発症する割合 P(B)=(a+b)/(a+b+c+d)
AとBが互いに独立である場合 P(A⋀B)=P(A)*P(B)
X2検定(独立性の検定)の基礎知識
X2検定は独立性の検定とも呼ばれます。「AとBが互いに独立である」を帰無仮説とします。つまり、帰無仮説が成り立つ場合はP(A⋀B)=P(A)*P(B)の関係が成り立ちます。
例として喫煙(要因)と肺癌(疾患)の関連を見てみます。
ある集団での喫煙率が20%、肺癌の発症率が10%であった場合、喫煙と肺癌が互いに独立した因子であると仮定すると図2のようなクロス集計表となります。喫煙あり群、なし群両者において肺癌の発症率は10%です。
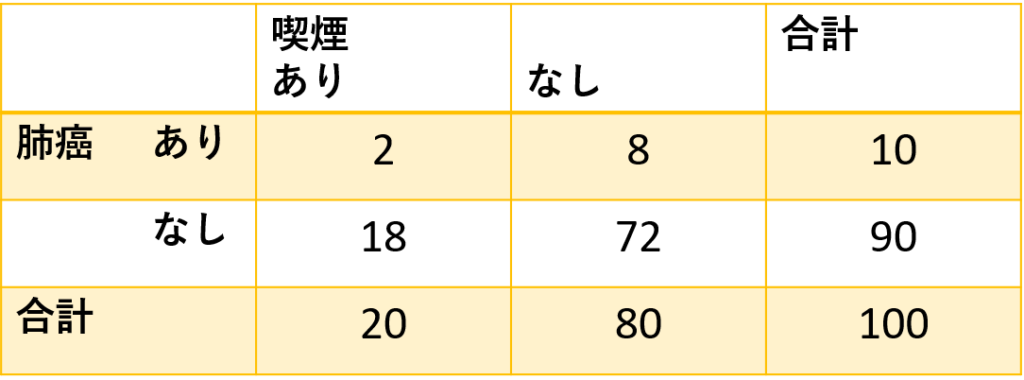
しかし、同じ喫煙率20%、肺癌発症率10%でも実際には図3のようになっていました(大げさすぎる例えですが)。
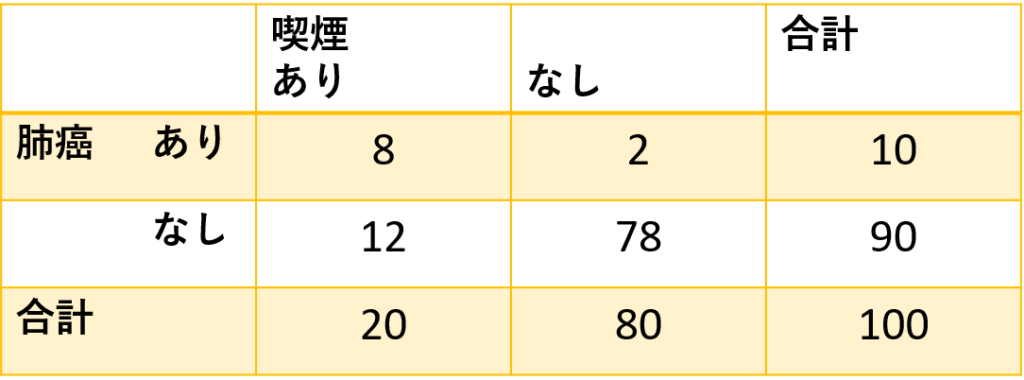
喫煙あり群では肺癌の発症率が8/20×100=40%、喫煙なし群では2/80×100=2.5%となっています。これが有意な差なのかどうかをX2検定を行うことで見ています。
ここで図2のようにAとBが互いに独立であると仮定したときのセルの度数を期待度数と呼びます。
X2検定の細かい説明は省きますが、X2分布というデータの2乗をすべて足し合わせてできた分布をクロス集計表に当てはめたピアソンのX2分布がベースとなっています。
Fisherの正確検定を使うとき
X2検定と同様、Fisherの正確検定も従属変数と独立変数が名義変数の場合に使用しますが、以下の場合はX2検定ではなく、Fisherの正確検定を用います。
- 全体のサンプル数が20未満である場合(図1ではa+b+c+d<20)
- いずれかのセルの期待度数が5未満となる場合
- 2×2以上のクロス集計表の場合(どの検定を使うかは諸説あります)
図2の期待度数を計算してみましょう。喫煙あり、肺癌ありの左上セルの期待度数は20×10/100=2と5を下回っているので、Fisher正確検定を使用したほうがよさそうです。
X2検定とFisherの正確検定の実際
SPSSを使ったX2検定とFisherの正確検定はこちら>>SPSSで単変量解析② X2(カイ二乗)検定とFisherの正確検定
Stataを使ったX2検定とFisherの正確検定はこちら>>Stata単変量解析②-χ<sup>2</sup>(カイ二乗)検定とFisherの正確検定


コメント