3群間で検定を行う場合、2群間の検定を3回行うことには問題があり、t検定やMann-Whitney検定を用いることはできません。そのため、分散分析(ANOVA)の手法を用います。
分散分析の基礎についてはこちら>>3群間の比較(分散分析:ANOVA)の基礎知識
実際にSPSSで3群間の比較をやってみましょう。
一元配置分散分析(one way ANOVA)
比較する変数が正規分布に従う場合には一元配置分散分析(one way ANOVA)を用います(パラメトリック検定)。
今回の例ではBMIを3群に分けて、3群間でエコーで測る左心房の大きさ(LAD)に違いがあるかを見ていきます。つまり、従属変数:LAD、独立変数:BMI(1:BMI 20未満、2:BMI 20以上25未満、3:BMI 25以上)です。
分析➡平均の比較➡一元配置分散分析
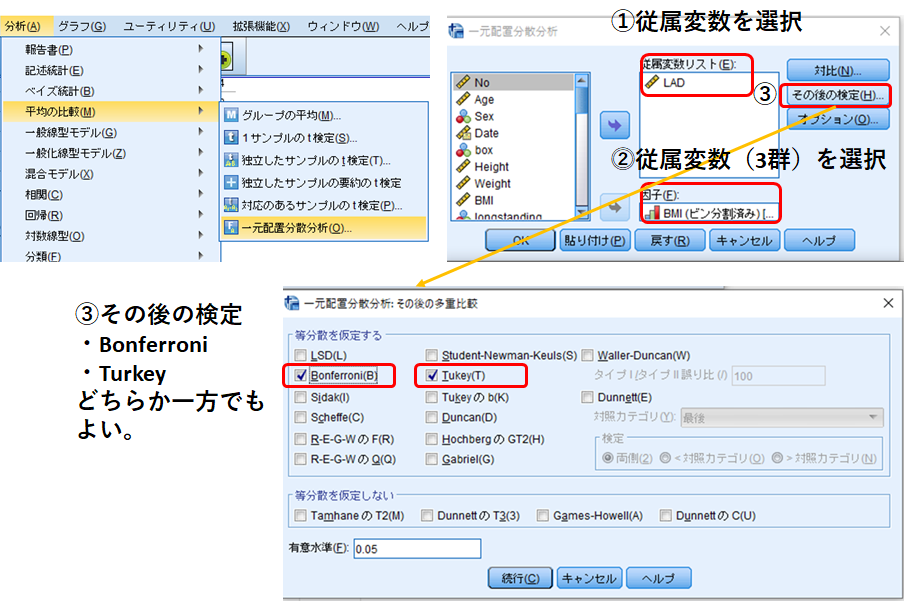
従属変数、独立変数をそれぞれ入力します。[その後の検定]ではBonferroniもしくはTurkeyを選択します。2つの違いについてはこちらを参照してください。>>3群間の比較(分散分析:ANOVA)の基礎知識
分散分析の結果と多重比較法(post hoc test)が両方出力されます。
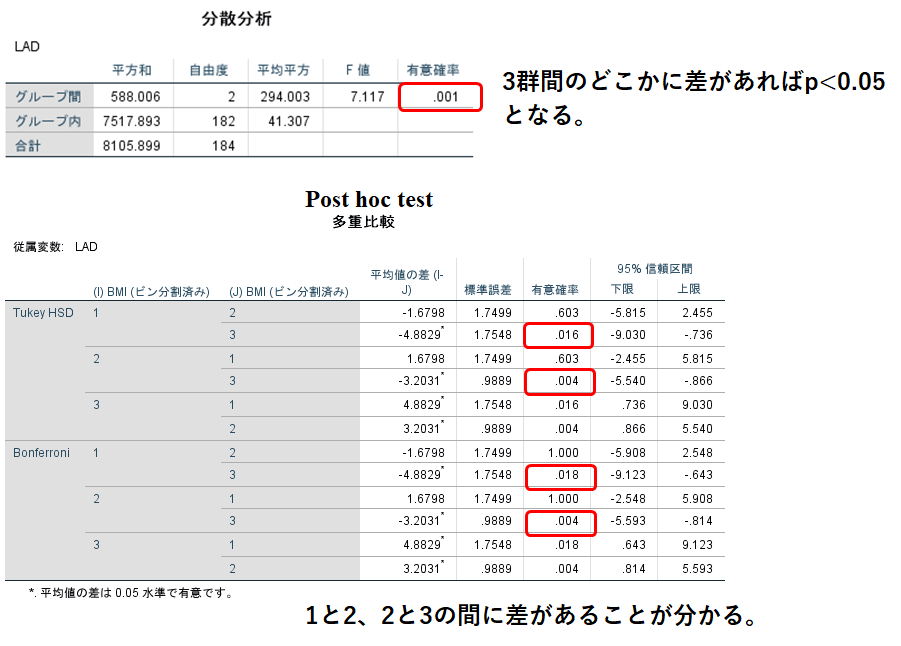
分散分析のグループ間は群間変動、グループ内は郡内変動を示しています。ここででる有意確率 p<0.05であった場合は、3群のどこかに差があるということを示しています。
多重比較法の表では1 vs 2, 2 vs 3, 3 vs 1でどこに差があるのかを確認することができます。
多重比較の表では1(BMI 20未満)と3(BMI 25以上)、2(BMI 20以上25未満)と3(BMI 25以上)の間に有意な差があることがわかります。
Kruskal-Wallis検定
ノンパラメトリックな手法としてKurskal-Wallis検定があります。
先ほどと同じ例を用います。実際には左心房の大きさ(LAD)は正規分布に従うので、パラメトリック検定を用いるのが正しいです。
分析➡ノンパラメトリック検定➡独立サンプル(ここまではMann-Whitneyの検定のときと同様です。)
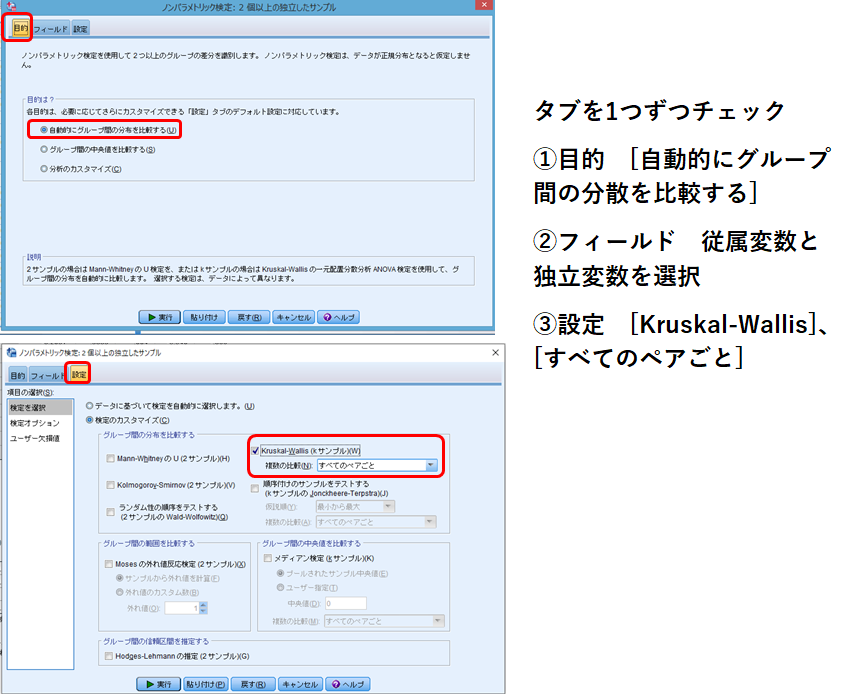
左上のタブを一つずつクリックして、チェックしていきます。
こちらも3群間の検定と多重比較法の結果が同時に出力されます。
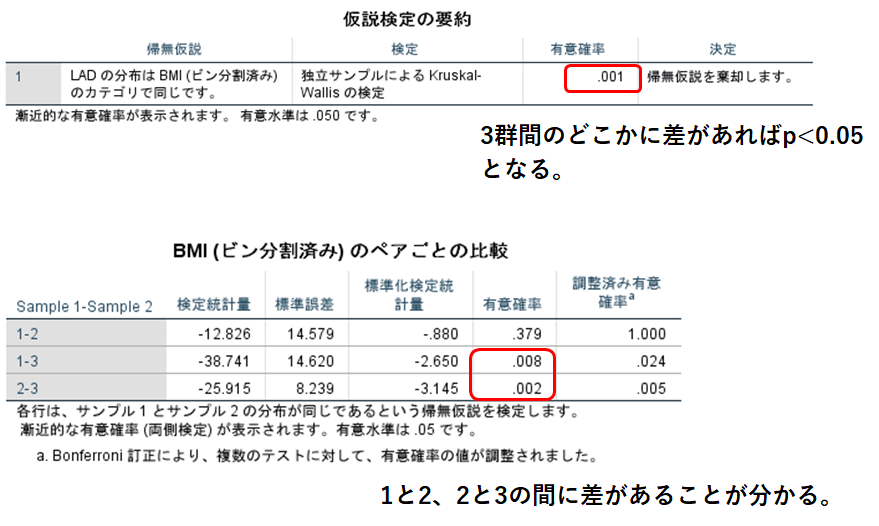
一元配置分散分析のとき結果の解釈は同様で、p<0.05は3群のどこかに差があるということを表しており、どこに差があるかは多重比較法の結果を見ます。
一元配置分散分析、Kruskal-Wallis検定ともに3群だけでなく群の数が増えても同様に検定できます。


コメント