SPSSで比例ハザード分析

生存分析の多変量解析が比例ハザード分析です。単変量解析が終わったら、多変量解析を行いましょう。
生存分析の基礎はこちら>>生存分析の基礎
生存分析（単変量解析）、Kaplan-Meier曲線の描き方はこちら>>SPSSで生存分析

独立変数の選び方

多変量解析は複数の因子のなかで従属変数に対して、独立変数がどの程度影響を与えているかや交絡因子を除くために行います。独立変数の選び方はロジスティック回帰分析のときと同様です。変数の種類や分布に制限はありません。

Cox比例ハザードモデル

生存分析のときと同じデータセットを用います。単変量解析ではDrug Aが心不全再入院を有意に減少させることがわかりました。他の因子を入れて解析しても同様の結果が得られるのかどうか、アウトカムである心不全再入院にどの程度寄与しているかどうかをみていきます。

この例ではN=319、うち再入院が84であったので、最大で84/7-10=8-12個を入れることができます。

分析➡生存分析➡Cox回帰

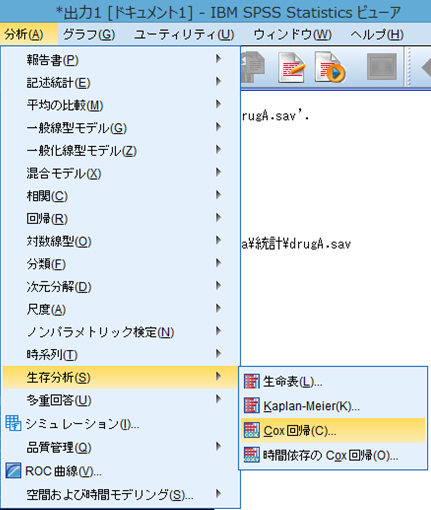
ここでは年齢、性別、今回の研究のメインであるDrug Aの他、これまでに心不全再入院と関与があると報告されているEF（駆出率）、BNPを選択します。

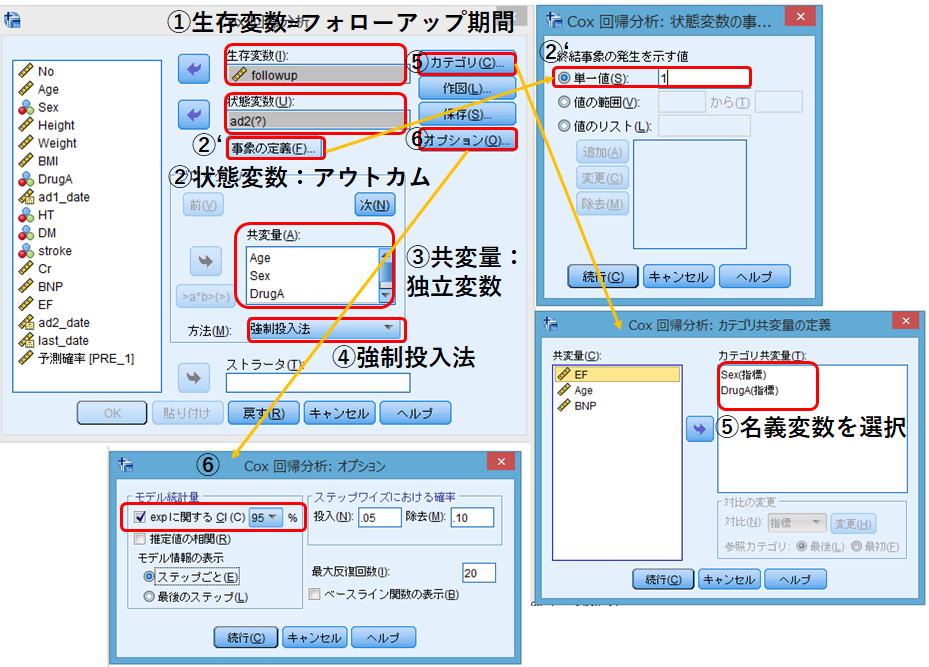
①生存変数：フォローアップ期間を入力。

②状態変数：アウトカム　ここでは”ad2”

②´事象の定義：[単一値]にチェックし、[1]を入力し、[続行]。アウトカムありに設定した方を入力します。ここではアウトカムあり=1としているため、[1]。

③共変量：独立変数を入力。

④方法：[強制投入法]を選択。

⑤カテゴリ：③共変量で選択した独立変数のうち、名義変数を選んでカテゴリ共変量のBoxに入れて、[続行]。

⑥オプション：[expに関するCI]にチェックし、[95]%を入力し、[続行]。

上記を入力したら、[OK]で出力されます。

結果の解釈

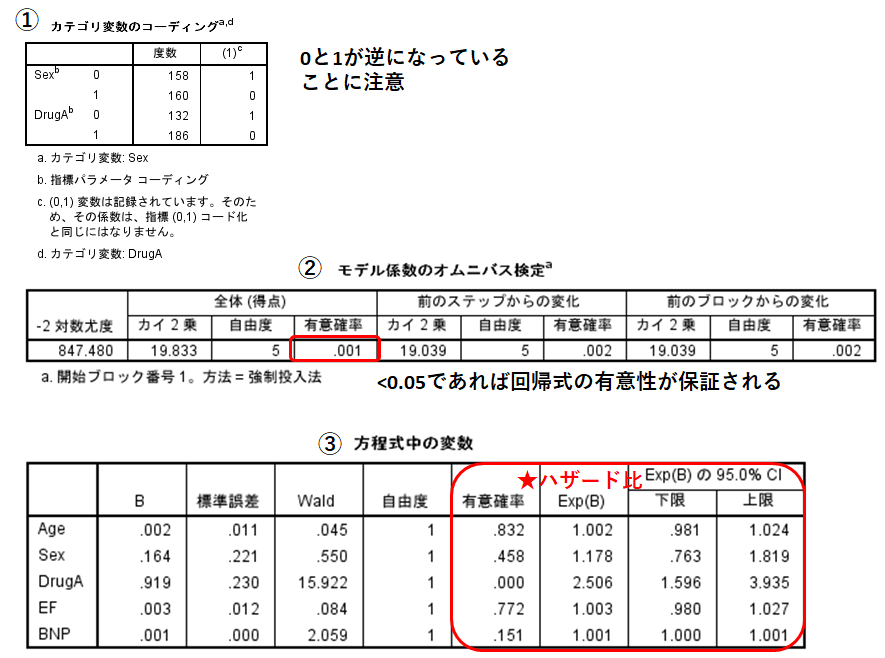
①カテゴリ変数のコーティング：ここでは入力した0と1が逆転していることに注意します。

②モデル係数のオムニバス検定：p<0.05であれば回帰式の有意性が保証されます。 ③方程式中の変数：ここではExp(B)はハザード比で、ある一定時間において独立変数が1上がるごとに何倍のリスクがあるかを示しています。95%信頼区間と有意確率も出力されています。

今回の関心事であるDrug Aの項目を見てみましょう。ハザード比は2.51（95%信頼区間：1.60-3.94）となっています。データセットでは「Drug A　1：あり、0：なし」としていましたが、①からわかるように式中では0と1が逆転しています。式中では「Drug A　0：あり、1：なし」と定義しなおされているのです。そのため、Drug Aは変数が1上がると、つまりDrug Aの使用なしでは使用ありに比べて2.51倍再入院のリスクが上昇するという解釈になります。