ROC曲線(Receiver Operating Characteristic)とは何か?について前回お伝えしました。→ROC曲線って何?
今回は実際にロジスティック回帰分析で作ったモデルの精度を評価してみましょう!
ロジスティック回帰分析を行いたい方はこちら→SPSSでロジスティック回帰分析
ROC曲線で精度を評価したいとき
ROC曲線を描く前に、どのようなときにこの解析が必要となるか考え、正しく使用しましょう。
ROC(Receiver Operating Characteristic) 曲線とは、アウトカムを予測するモデルを作ったとき、どの程度そのモデルが正確に予測しているか、推定値と観察値を比較したものです。「作ったモデルを評価する」ときに使用します。
新規にモデルを作った場合に精度を評価したり、既存の予測モデルに新規の項目を追加して、予測能がどの程度よくなるかを比較したりするのに使います。同じロジスティック回帰分析でもAとBの関連をみることが目的という場合には必要ありません。
ロジスティック回帰分析の際にROC曲線を描く準備をする
まず、ロジスティック回帰分析を行います。ロジスティック回帰分析の詳細はこちら→SPSSでロジスティック回帰分析
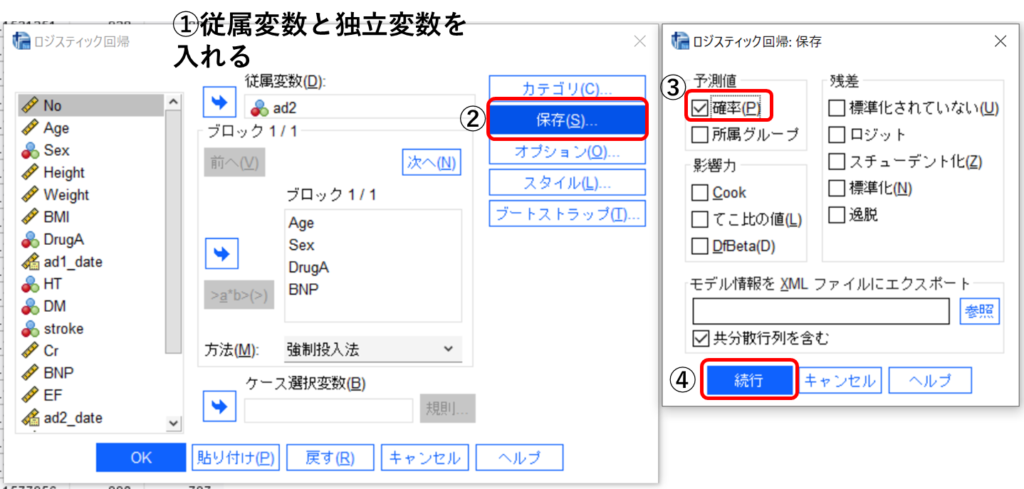
ROC曲線を描く場合には通常の従属変数と説明変数を入れた後に、[保存]をクリックし、予測値の[確率]にチェックを入れます。
ROC曲線を描く
分析➡分類➡ROC曲線
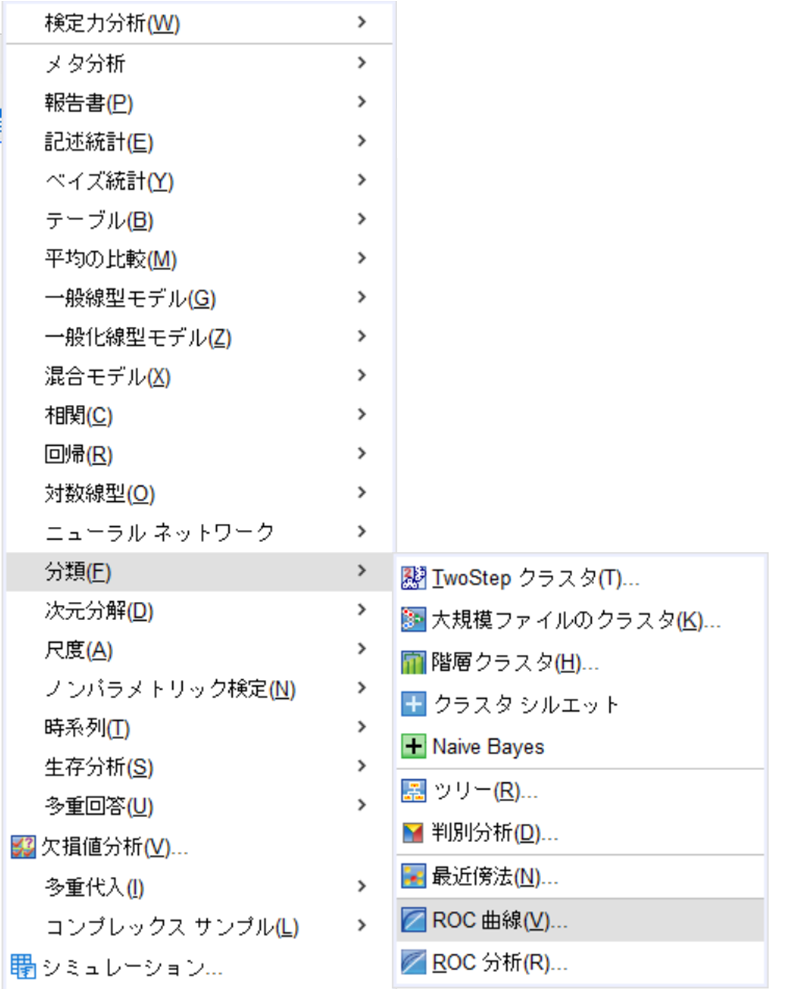
先ほどロジスティック回帰分析の際に保存を行ったので、左側のボックスの中に[予測確率]という項目ができていると思います。(※例ではモデルを2つ保存したので[予測確率]が2つできています。)
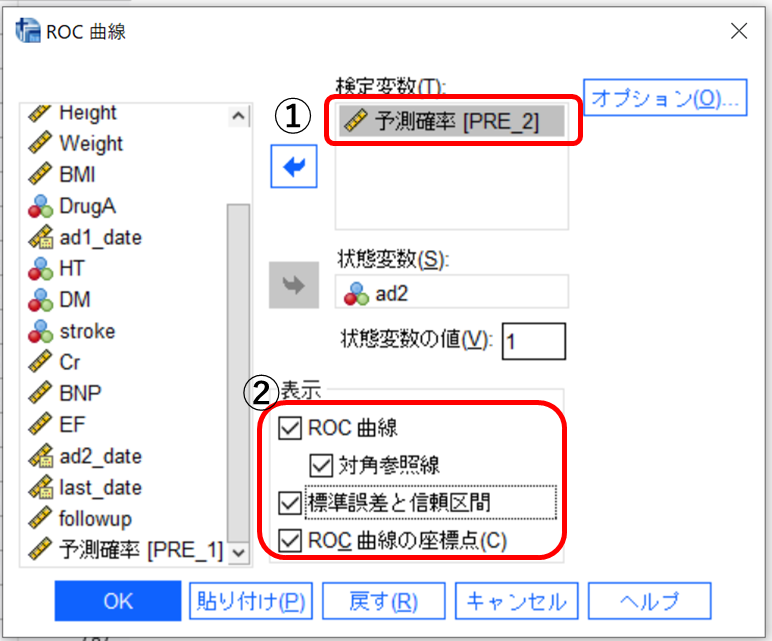
① 検定変数に[予測確率]を入力します。
② 表示の[ROC曲線]、[対角参照線]、[標準誤差と信頼区間]、[ROC曲線の座標点](こちらはなくてもOK)にチェックを入れて[OK]をクリックします。
結果の解釈
ROC曲線が表示されます。
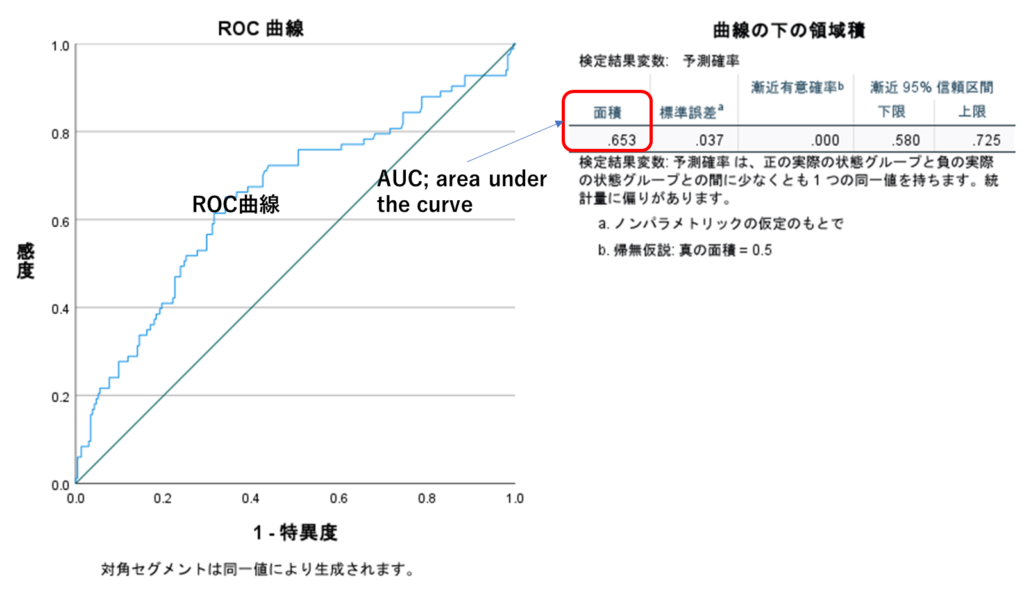
曲線下の領域積の[面積]にあたる部分がAUC (area under the curve)です。AUCはc-statisticsとも言われます。このモデルはAUC 0.65なので、poorであまりよい予測モデルとは言えません。
| AUC | 判断 |
| 0.9-1.0 | Excellent |
| 0.8-0.9 | Good |
| 0.7-0.8 | Fair |
| 0.5-0.7 | Poor |
| 0.5 | Random |
| <0.5 | Worse than random |
複数のモデルを比較したい
2つのモデルを比較してみましょう。
「ロジスティック回帰分析の際にROC曲線を描く準備をする」の項目のところで比較したいモデルを別々に2つ保存します。
分析➡分類➡ROC分析
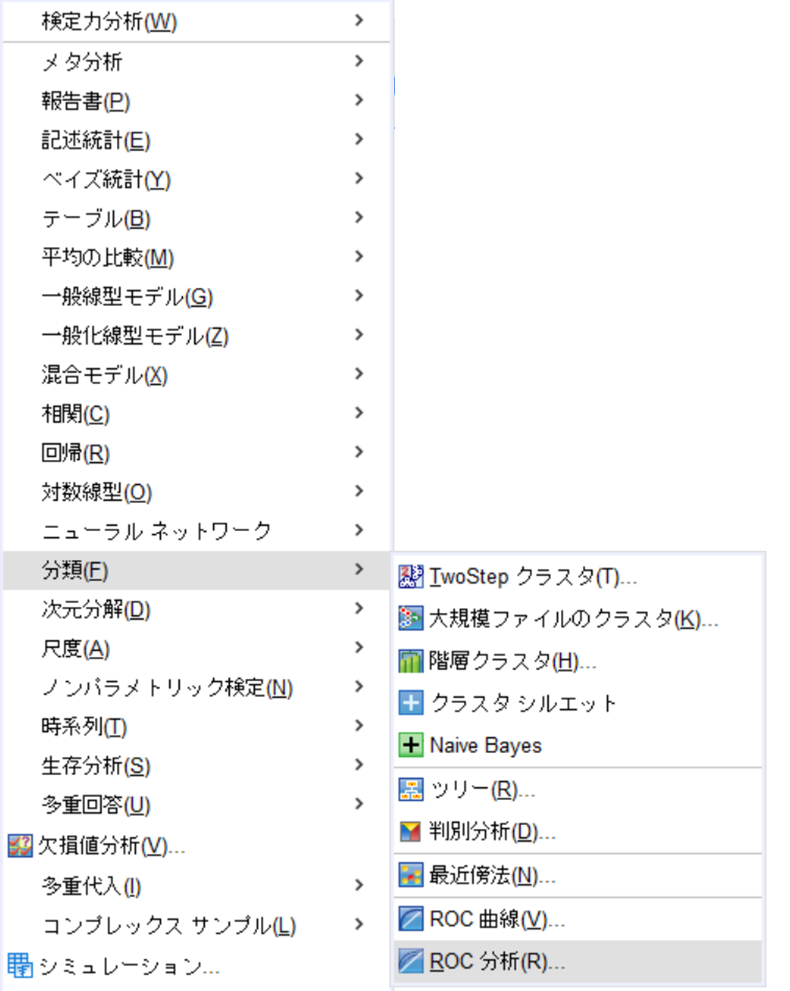
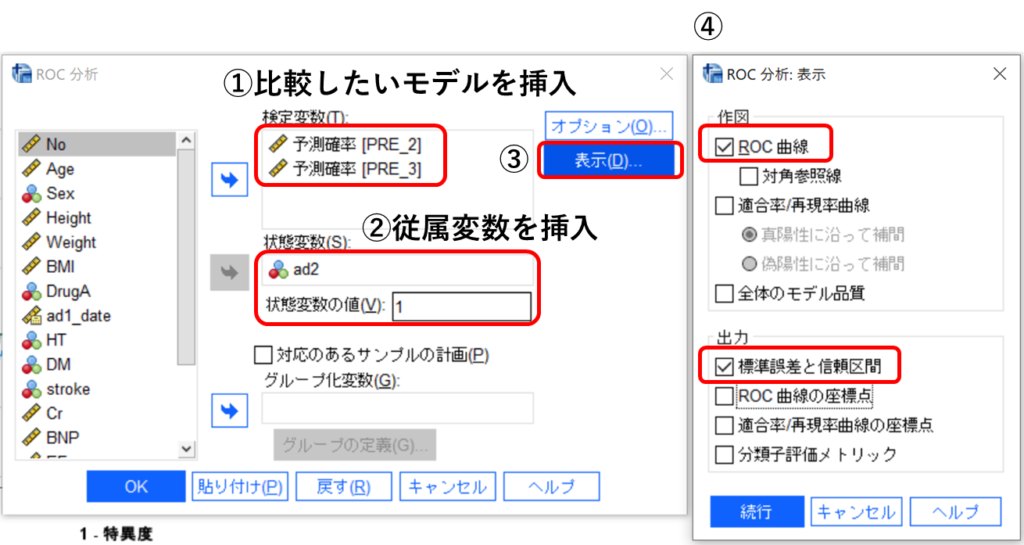
① 検定変数に比較したいモデルを挿入。
② 状態変数に従属変数(アウトカム)を挿入、アウトカムは0、1の二値数で1をアウトカムありとしているので[1]を入力。
③ [表示]をクリック。
④ [ROC曲線]と[標準誤差と信頼区間]をクリックして[続行]。
⑤ [OK]をクリック。
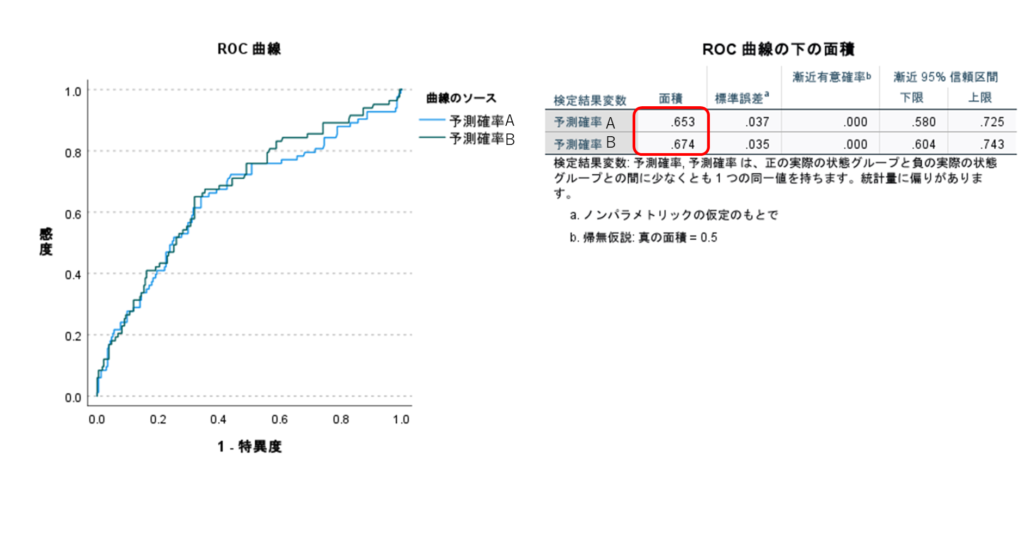
2つのROC曲線、AUCが同時に表示されます。
ただし、一般的にはモデルの項目を増やすとAUCは大きくなる方向に働くということ、作成したモデルに使用したサンプルでは当てはまりがよく出てしまうので(過大評価してしまう)、別のサンプルで評価を行う必要があることには注意が必要です。こちらは成書に譲ります。



コメント
わかりやすい説明ありがとうございます.
この手順に従ってROC曲線を描いて思ったのですが、ロジスティック回帰分析で複数の独立変数を入れている状態ですから、この曲線がどの項目の曲線なのか?・・・と困惑してしまいました。無知ですみません。
【有意】で、【最も影響度の高い】項目が自動的に選ばれたROC曲線なのでしょうか?
ご質問いただき、ありがとうございます。
この例の場合は、ロジスティック回帰分析の予測確率を用いていますので、回帰式に用いたすべての変数が考慮されています。
ロジスティック回帰分析の予測確率については別ページSPSSでロジスティック回帰分析の後半に記載しています。
すべての変数が考慮されるため、関係のない変数を入れてしまうと予測精度が下がってしまうこともあります。
独立変数単独のAUROCを算出したい場合は、単独の変数を選択します。
病気の診断を行うにあたり、検査値のカットオフ値を求めたいと考えています。ROC解析を行い、AUC、感度・特異度を求めモデルの精度を求めたいと考えていました。しかし、検査値が正規分布を示しません。
この場合、どのような解析をすればいいのでしょうか。
結果を論文に示す場合に、ROC解析ができないのであれば、単純に感度・特異度を求め、そこからカットオフ値を算出、モデルの精度は示さないのもありでしょうか。
ROC曲線は感度と特異度をプロットしたものです。
正規分布を仮定していませんので、検査値の分布によらず使用することが可能です。
カットオフ値の選び方は①ROCの最も左上に近い点を選ぶ②ヨウデン指数を用いる③手動で設定する
などの方法があります。
どのような目的の検査なのか(感度・特異度のバランスが良い方がいい、ルールアウトに使用したいので感度を高くしたい)、目的に応じて使い分けるとよいと思います。